
Le soluzioni del 14 agosto 2023 a cura di Fabio Ciuffoli
Ieri abbiamo proposto tre problemi sulle condizioni di equilibrio e ora pubblichiamo le soluzioni.
Sospesi in equilibrio – soluzioni
1. Il sistema in figura è in equilibrio. La scatola b pesa 73,5 kg. Quanto pesano le scatole a, c, e d? (non si tiene conto del peso di fili e bracci) 2. SOLUZIONE. A partire dal basso, avremo il seguente sistema di equazioni:
2. SOLUZIONE. A partire dal basso, avremo il seguente sistema di equazioni:
svolgendo e sostituendo
I valori sono approssimati al secondo decimale ma, come suggerisce Giorgio Vecchi, potremmo scriverli in forma frazionaria: a = 49/9; c = 343/18; d = 49/9.
2. Collocare nelle nove scatole, contrassegnate con le lettere a, b, c, … h, i, i nove pesi di 1 kg, 2 kg, 3 kg, … 8 kg, 9 kg, uno per scatola in modo che il sistema illustrato in figura sia in equilibrio. Quale peso va collocato nella scatola con la lettera a? [non si tiene conto del peso di fili, bracci e scatole].
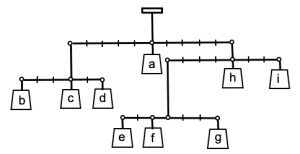
2. SOLUZIONE. Per l’equilibrio del braccio “imperniato” su c, deve risultare 3b = 2d. Per l’equilibrio del braccio inferiore, deve risultare 3g = 3e + f. Per l’equilibrio del braccio “imperniato” su h, abbiamo 3i = 4(e + f + g). Infine per l’equilibrio del braccio “imperniato” su a, abbiamo b + c + d = e + f + g + h + i.
Dalla terza uguaglianza apprendiamo che i è divisibile per 4. Non può essere i = 4 (perché altrimenti sarebbe e + f + g = 3 con e, f, g diversi) e allora i = 8. Ne segue: e + f + g = 6 e quindi: e, f, g, assumono valori nell’insieme (1, 2, 3). Analogamente, dalla prima uguaglianza, ricaviamo d = 6 (con b = 4) oppure d = 9 (con b = 6). A questo punto l’ultima uguaglianza si scrive come b + c + d = 6 + h + 8 ovvero b + c + d = 14 + h. Sostituendo i valori (b,d) = (4,6) si ottiene h = 5, c = 9, a = 7. Sostituendo (b,d) = (6,9) otteniamo c = 4, h = 5, a = 7. In ogni modo, nella scatola con la lettera a, va collocato un peso di 7 kg.
3. Quali sono i pesi (interi <140) da sostituire alle lettere, dalla a alla f, affinché il sistema sia in equilibrio? [non si tiene conto del peso di fili, bracci e scatole].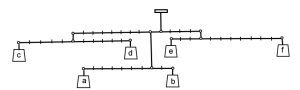
3. SOLUZIONE. Avremo: 7a = 2b; 3e = 8f; 6d = 5c; 9(c + d) + (a + b) = 4(e + f). Svolgendo: b = 7a/2; f = 3e/8; d = 5c/6.
Ora sostituendo: 9(c + 5c/6) + (a + 7a/2) = 4(e + 3e/8)
che diviene: 9(11c/6) + (9a/2) = 4(11e/8)
semplificando: 33c + 9a = 11e da cui a = 11(e – 3c)/9
a deve essere multiplo di 11 e di 2, b multiplo di 7, c multiplo di 6, d multiplo di 5, e multiplo di 8, f multiplo di 3.
a = 22; b = 77; c = 18; d = 15; e = 72; f = 27.
a = 44 è da escludere perché b supererebbe 140.
I Giochi del Lunedì tornano tra due settimane.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).