Menu
Le soluzioni del 31 luglio 2023 a cura di Fabio Ciuffoli
Ieri abbiamo proposto due problemi tratti dal blog Datagenetics e di seguito pubblichiamo le nostre proposte di soluzione.
L’arrivo di un treno – soluzioni
1. Due gemelli, dopo aver percorso un quarto del tunnel, sentono alle loro spalle l’arrivo di un treno che si sta avvicinando. Non sanno quanto sia lontano il treno, ma sanno che il tunnel è troppo stretto e quindi devono uscire rapidamente. Antonio decide di tornare di corsa all’ingresso e riesce appena ad uscire in sicurezza. Eugenio decide di correre verso l’uscita in fondo al tunnel e anche lui riesce appena ad uscire sano e salvo prima che arrivi il treno. Se entrambi i ragazzi corrono alla stessa velocità costante di 24 km/h e anche il treno viaggia a velocità costante, qual è la velocità del treno?
1. SOLUZIONE. Presentiamo due metodi per la soluzione, il primo analitico descrittivo e il secondo logico intuitivo.
A. Definiamo t la lunghezza del tunnel in km, d la distanza del treno dall’inizio del tunnel in km e s la velocità del treno in km/h, come schematizzatoin figura.
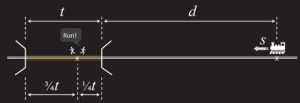
Sappiamo che ciascuno dei gemelli corre a 24 km/h. Antonio torna all’inizio del tunnel, quindi deve percorrere una distanza di t/4 km. Poiché la sua velocità è di 24 km/h, il tempo impiegato è t/96. Sappiamo che riesce a uscire appena in tempo, quindi il treno arriva all’ingresso del tunnel nello stesso istante. Il tempo impiegato dal treno è d/s. Uguagliando le due equazioni otteniamo ts = 96d. (1) Eugenio va nella direzione opposta e percorre una distanza di 3t/4, alla stessa velocità di suo fratello, 24 km/h. Il tempo impiegato è 3t/96 e anche lui esce appena in tempo, quindi il treno sarà all’uscita del tunnel nello stesso istante in cui Eugenio sta uscendo. Per arrivare all’uscita, il treno ha dovuto percorrere d + t km, quindi il tempo impiegato è (d + t)/s, e questo deve essere lo stesso tempo della corsa di Eugenio. Uguagliando otteniamo 3ts = 96(d + t). (2) A questo punto, sostituendo la (1) nella (2) otteniamo il risultato che è 2d = t. Il tunnel è lungo il doppio della distanza dal treno all’ingresso del tunnel e il treno viaggia a 48 km/h.
B. C’è un altro metodo che non richiede equazioni simultanee, ma solo un po’ di logica e di buon senso. Sappiamo che Antonio inizia a ¼ del percorso nel tunnel e se corre verso l’ingresso ha percorso ¼ della lunghezza del tunnel nel tempo che il treno impiega per arrivare all’ingresso del tunnel. Se fosse andato verso l’uscita, avrebbe percorso esattamente metà del tunnel mentre il treno sarebbe arrivato all’inizio del tunnel. Ora affinché il ragazzo e il treno siano all’uscita contemporaneamente, è abbastanza chiaro che il treno deve viaggiare esattamente al doppio della velocità del ragazzo perché deve percorrere il doppio della distanza nello stesso tempo.
2. Nel diagramma seguente, un triangolo è disegnato su una serie di linee parallele equidistanti. Se il rapporto delle regioni C /B è 11/5 qual è il rapporto delle regioni D/A? Nota: I vertici del triangolo non si trovano su nessuna delle linee.
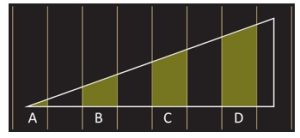Il disegno non è in scala2. SOLUZIONE. Consideriamo i trapezi rettangoli color verde in B, C e D. Definiamo x la distanza orizzontale tra il vertice in A e il punto medio in B, quindi la distanza tra A e il punto medio in C sarà (x + 2) come in figura seguente.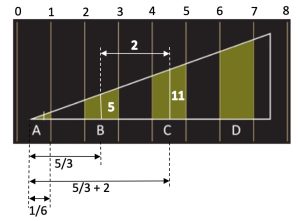 
Per i triangoli simili avremo x : (x + 2) = 5 : 11. Svolgendo x = 5(x + 2) / 11 che diviene x = 5/3. Ora possiamo calcolare la base del triangolo rettangolo verde in A che è (5/3 – 1,5) = 1/6 e il suo punto medio sarà 1/12. Ancora con i triangoli simili, possiamo calcolare la perpendicolare dal punto medio della base del triangolo rettangolo verde in A, che chiamiamo y e sarà 1/12 : 5/3 = y : 5 da cui y = 1/4. Nuovamente con i triangoli simili possiamo calcolare il segmento perpendicolare in D che chiamiamo k e sarà 5/3 : (5/3 + 4) = 5 : k da cui k = 17. L’area verde in D è 17 * 1 = 17, l’area vede in A è 1/6 * 1/4 = 1/24. Infine rapporto tra le aree verdi in D e in A è [17 / (1/24)] = 408.
Un altro metodo per arrivare alla soluzione utilizza la trigonometria. Indicando con a l’ascissa del punto A (origine in corrispondenza della prima linea verticale) con alfa l’angolo formato dalla retta con l’orizzontale e assumendo unitaria la distanza fra le rette si ottiene:
Area C/Area B = (1 – a + 3 + 1 – a + 4)d tan(alfa) /(1 – a + 1 + 1 – a + 2)d tan(alfa) = 11/5. Da cui a = 5/6. Il rapporto fra le aree delle regioni D e A è (1 – a + 5 + 1 – a + 6)tan(alfa) / [(1 – a)(1 – a)tan(alfa)] = 68 x 6 = 408
I Giochi del Lunedì tornano tra due settimane.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).