Menu
I Giochi del Lunedì di Prisma del 31 luglio 2023 – L’arrivo di un treno
Oggi presentiamo due stimolanti problemi, segnalati dal blog Datagenetics, che si possono risolvere con diversi metodi. Invitiamo i lettori a inviarci osservazione e proposte di soluzione nello spazio riservato ai commenti. Domani alle ore 17.00 pubblicheremo le nostre soluzioni commentate.
L’arrivo di un treno
1. Due gemelli, dopo aver percorso un quarto del tunnel, sentono alle loro spalle l’arrivo di un treno che si sta avvicinando. Non sanno quanto sia lontano il treno, ma sanno che il tunnel è troppo stretto e quindi devono uscire rapidamente. Antonio decide di tornare di corsa all’ingresso e riesce appena ad uscire in sicurezza. Eugenio decide di correre verso l’uscita in fondo al tunnel e anche lui riesce appena ad uscire sano e salvo prima che arrivi il treno. Se entrambi i ragazzi corrono alla stessa velocità costante di 24 km/h e anche il treno viaggia a velocità costante, qual è la velocità del treno?
2. Nel diagramma seguente, un triangolo è disegnato su una serie di linee parallele equidistanti. Se il rapporto delle regioni C/B è 11/5 qual è il rapporto delle regioni D/A?
Nota: I vertici del triangolo non si trovano su nessuna delle linee.
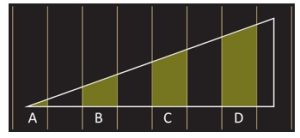Il disegno non è in scala.Aggiornamento per le soluzioni click qui.
I due problemi sono tratti e riadattati dal blog Datagenetics. Il secondo problema ha fatto parte delle prove dell’American Invitational Mathematics Examination (AIME) del 2016.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
19 risposte
Pongo la distanza fra le linee verticali, quindi anche la base dei vari trapezi B – C – D = 1.
Chiamo x la base del triangolino di area A:
11 : 5 = (x+3,5) : (x + 1,5)
da cui x = 1/6
L’altezza h del triangolino A è:
h : 5 = 1/6 : (1,5 + 1/6)
da cui h = 1/2
Ne consegue che l’area A è = (1/6*1/2)/2 = 1/24
L’altezza H e quindi anche l’area D (essendo la base=1) è:
(1/6 + 1,5) : 5 = (1/6 + 5,5) : H
da cui H = D = 17
Perciò: D/A = 17/(1/24) = 408
Problema 2. Risultato 408. Vedi svolgimento allegato
Risposta quesito 1: 48 km/h
Risposta quesito 2: 408, allego procedimento sperando sia corretto.
Ottimo. A domani per le soluzioni commentate
Errata Corrige: La coordinata del vertice sinistro è (d, 0)
Secondo problema. 408. Indicando con a la distanza fra il vertice del triangolo e la retta verticale a sinistra e con d le distanze fra le rette si ottiene area C/ area B = (9d-2a)/(5d-2a)=11/5 da cui d=6/5a. Il rapporto area D/ area A = (13d-2a)d/(d-a)^2 = 408. Il disegno non sembrerebbe in scala.
Sì è vero, il disegno non è in scala e andava specificato, ma noi abbiamo riproposto l’originale così come è, senza alcuna specificazione.
Primo 48 km/h
Secondo 408
Il primo è facile. È perfetto il ragionamento di Raffaella Fiorini.
Il secondo è più tosto. Non ho tempo per scrivere la soluzione completa, a me viene 37^2 ma potrei aver fatto errori di calcolo.
Dato che i gemelli hanno la stessa velocità, quando Antonio arriva all’ingresso, Eugenio sarà a metà galleria. Quindi dato che Eugenio e il treno arrivano all’uscita contemporaneamente e il treno percorre una distanza doppia rispetto ad Eugenio, significa che il treno ha una velocità doppia rispetto a quella di Eugenio
2 – Diagramma: 17/5.
I segmenti verticali sono direttamente proporzionali ed essendo le rette verticali equidistanti, aumentano delle stesse quantità (andando verso destra).
Quindi anche le aree dei trapezi (ogni volta di 6/5 del trapezio B). Si ottiene 17/5.
Per spiegarlo graficamente (ideale per i ragazzini):
Si potrebbe scomporre la figura in rettangoli e triangoli, osservando che il trapezio C contiene un rettangolino in più rispetto a B (pari a 6/5 di B). Anche D ha un rettangolino (identico) in più rispetto a D: altri 6/5 di B e si ottiene 17/5 (di B).
Per il “vero matematico”:
sia x il segmento orizzontale base del triangolino A
poniamo uguale a 1 la distanza tra le rette parallele (senza nulla togliere alla generalità: basta usare l’unità di misura opportuna)
sia y il rapporto di similitudine tra segmenti verticali e orizzontali (è la tangente dell’angolino di sinistra).
Abbiamo:
base minore di B =(x+1)y
base maggiore di B = (x+2)y
base minore di C =(x+3)y
base maggiore di B = (x+4)y
Calcoliamo le aree e poniamo il rapporto=11/5
Risolvendo si ottiene x=1/6
Ora si può calcolare il rapporto tra D e A…
1 – Treno
C’è già la risposta/spiegazione, sia semplice che da vero matematico.
Osservazione: se ci “dimentichiamo” di dire che i gemelli erano a 1/4 del tunnel quando sentono il treno e “cominciamo a correre”, il problema diventa “indeterminato” nel senso che il treno potrebbe avere qualunque velocità maggiore di 24km/h, (in base alla posizione raggiunta dai ragazzi)
Curioso, vero?
Non sono d’accordo sulla soluzione del problema n. 2. A domani per le soluzioni commentate.
1) 48 km che è il doppio della velocità dei ragazzi perché il treno entra nel tunnel quando uno dei ragazzi è a metà e lo percorre quindi a velocità doppia dei ragazzi
2) 15/1 ho fatto un ragionamento sulla somma basi dei trapezi essendo l’altezza la stessa
Ottima la prima risposta, sulla seconda c’è qualcosa da rivedere. A domani per le soluzioni commentate.
Mettendo l’origine nell’ingresso del tunnel e verso positivo concorde con la velocità del treno abbiamo le seguenti leggi orarie
XT=-L+VT×T
XA=D-V×T
XE=D+V×T
Dove lo 0 del tempo è l’istante in cui i gemelli sentono il fischio.
Siano T1 e T2 rispettivamente il tempo in cui il treno giunge all’ingresso del tunnel (insieme con Antonio) e il tempo in cui il treno giunge all’uscita del tunnel (insieme con Eugenio). Abbiamo quindi le seguenti equazioni
0=-L+VT×T1
0=D-V×T1
4D=D+V×T2
4D=-L+VT×T2
Dividiamo tutte le equazioni per D e definiamo l = L/D, t1=T1/D, t2=T2/D
0=-l+VT×t1
0=1-V×t1
4=1+V×t2
4=-l+VT×t2
Abbiamo quindi 4 equazioni in 4 incognite di cui una è la velocità del treno VT. Problema risolto
problema 2. Il treno viaggia a 48 km orari. Infatti, correndo a 24 km orari, mentre il primo fratello raggiunge l’ingresso del tunnel, il secondo giunge a metà del tunnel. In quel momento il treno imbocca tunnel. Se il treno raggiunge il secondo fratello proprio all’uscita del tunnel, avrà percorso tutta la galleria nel tempo in cui egli ne percorre mezza, dunque viaggia a velocità doppia rispetto ai ragazzi.
1°) 52
2°) 48 Km/h
Sul primo ho altri risultati, ti chiedo gentilmente il procedimento se vuoi…
L’ho risolto facendo questo ragionamento :
Suppongo la lunghezza del tunnel uguale a 96 km
Quando Antonio percorre 1/4 cioè 24 km in un’ora, il treno si trova all’imboccatura mentre Eugenio al 48 esimo km del tunnel.
A Eugenio gli rimangono da percorrere 48 km in due ore mentre al treno 96 km sempre in due ore cioè 48 km/h.
Quindi la velocità del treno è 48 km/h