Quantum day: perché il mondo è quantistico?

Il 2025 è stato ufficialmente incoronato “anno quantistico” e Prisma se ne è ampiamente occupata nel numero di gennaio e nei successivi con interviste, approfondimenti e dossier. Ma perché il nostro mondo è quantistico? Ce lo spiega Paolo Caressa

La natura sfuggente del mondo quantistico ha costituito un rompicapo per molte grandi menti. A partire da quella di Einstein che cercò di mostrare che l’universo non poteva essere quello descritto dalla meccanica quantistica. Si sbagliava e, da genio qual era, diede ai fisici quantistici le armi per riuscire a contraddirlo

Il fisico Richard Feynman, celebre per la creazione dell’elettrodinamica quantistica e per aver aperto la strada della moderna teoria quantistica dei campi, è divenuto una figura iconica della fisica del Novecento non solo per il suo genio scientifico ma anche per la sua enorme capacità divulgativa. Molti suoi libri sono infarciti dello stesso ironico umorismo che pervadeva le sue lezioni pubbliche. In una di queste, tenuta alla Cornell University nel 1964, il futuro Nobel per la fisica ebbe a pronunciare una celeberrima frase: “Posso sicuramente affermare che nessuno capisce la meccanica quantistica”.
Questa affermazione non vuol dire che nessuno capisce le equazioni e i concetti fisici che dal Novecento sono stati
proposti per spiegare i fenomeni quantistici ma che questi concetti sono alieni rispetto alla nostra intuizione, formatasi nell’esperienza del mondo macroscopico (o mesoscopico, come dovremmo dire, riservando l’aggettivo macroscopico al mondo dei sistemi stellari e delle galassie dove un’altra teoria, la relatività generale di Einstein, regna sovrana in un non meno controintuitivo mix non euclideo fra spazio, tempo e materia).
Feynman spiegò le sue perplessità in una lettera che inviò a David Mermin, un fisico molto meno noto: “Per tutta la mia vita matura ho cercato di distillare la stranezza della meccanica quantistica in maniere sempre più semplici”. Questa lettera, che è del 1984, ossia di 40 anni fa, si apre in un modo che, per chi l’ha ricevuta, vale quasi un premio Nobel perché Feynman si rivolge a Mermin in questi termini: “Uno degli articoli di fisica più belli che io conosca è il tuo, sull’American Journal of Physics […]. Da allora l’ho copiato quasi parola per parola (ovviamente attribuendotelo) in diverse conferenze recenti sull’argomento. Grazie”.
Che cosa c’è scritto in questo articolo, peraltro dal taglio divulgativo, per generare un tale moto di riconoscenza da parte del maggior esperto di fisica quantistica allora in vita? La meraviglia di Feynman è giustificata, visto che Mermin descrive un esperimento in grado di spiegare perché il mondo è quantistico.
La natura sfuggente del mondo quantistico ha costituito un rompicapo per molte grandi menti, a partire da quella di Einstein, uno dei primi ad abbracciare la nuova fisica con il lavoro del 1905 sull’effetto fotoelettrico che gli diede il Nobel. Ma un bias culturale del grande scienziato tedesco gli rendeva impossibile rinunciare al determinismo, assente invece nei principi quantistici, quali il celebre principio di indeterminazione di Heisenberg. Già nei suoi scambi polemici con Niels Bohr, nel carteggio con Max Born e soprattutto in alcuni suoi importanti lavori, Einstein cercò di mostrare che il mondo non poteva essere quello descritto dalla meccanica quantistica. Si sbagliava e, da genio qual era, diede ai fisici quantistici le armi per riuscire a contraddirlo.
Nel 1935, Einstein, assieme a Boris Podolsky e Nathan Rosen, pubblicò un articolo intitolato Può la descrizione quantistica della realtà dirsi completa?, nel quale descriveva un esperimento volto a mettere in crisi la descrizione quantistica del mondo reale come definitiva. Il trio di autori si denota oggi con la sigla EPR. I tre utilizzarono una caratteristica dei sistemi quantistici, quella di non poter essere in un ben preciso stato, ma in una “sovrapposizione di stati”. Semplificando, possiamo descrivere il paradosso EPR in questo modo: abbiamo un sistema di due particelle quantistiche, A e B, che si trova in uno stato che denotiamo con il numero 0. Questo stato è la somma di due stati x e y, che possono valere +1 o -1 e che devono soddisfare l’equazione x + y = 0.
Quando separiamo le particelle, esse continuano a permanere in questo stato 0 e, se misuriamo lo stato di una di loro, la meccanica quantistica ci dice che il processo di misurazione fa “collassare la funzione d’onda”, una locuzione lugubre per dire che la particella A, una volta misurata, si pone in un preciso stato, diciamo -1. A quel punto, misurando la particella B, la troveremo sicuramente nello stato +1, dato che la sovrapposizione deve continuare a fare 0. Questa sovrapposizione di stati può teoricamente essere mantenuta pur separando a una distanza arbitraria le due particelle, il che vuol dire che, misurando lo stato di A, istantaneamente, a qualsiasi distanza sia da B, lo stato di quest’ultima viene determinato.
Einstein, Podolsky e Rosen sottolinearono come questo fatto contraddicesse i principi della relatività, per i quali la portata di interazione di particelle, o di oggetti più grandi, è limitata al raggio d’azione dovuto all’insuperabilità della velocità della luce. La conclusione di EPR era che la meccanica quantistica, pur modellizzando correttamente alcuni fenomeni, non poteva descrivere completamente la realtà fisica perché violava il principio di località, cioè il fatto che quel che accade in un posto (come misurare un parametro di una particella) non può avere conseguenze istantanee su oggetti molto distanti. La conclusione di EPR era che l’unico modo per salvare il determinismo e la fisica quantistica al medesimo tempo è di supporre che esistano delle “variabili nascoste” che non compaiono nella fisica quantistica.
Nei decenni seguenti si è provato invece, prima in linea teorica e poi sperimentalmente, che è vero il contrario! Il fisico nord-irlandese John Bell ha dedotto, agli inizi degli anni Sessanta, una disequazione che deve essere soddisfatta da sistemi fisici con variabili nascoste che rispettano il principio di località, salvo poi mostrare come la meccanica quantistica può violarla! A queste idee, puramente speculative, seguì anche una verifica sperimentale compiuta dal francese Alain Aspect all’inizio degli anni Ottanta, cui seguirono quelle dell’americano John Clauser e dell’austriaco Anton Zeilinger, quest’ultimo uno dei padri della crittografia e del calcolo quantistici. I tre presero il premio Nobel per queste loro ricerche sperimentali nel 2022.
Ma torniamo di nuovo all’articolo di Mermin che tanto aveva colpito Feynman. In effetti, Mermin aveva trovato un modo particolarmente semplice di descrivere le disuguaglianze di Bell e gli esperimenti di Aspect. Proviamo a spiegare come.
Un “rilevatore di Mermin” è un dispositivo dotato di un interruttore – che può stare in una di tre posizioni disponibili (1, 2 e 3) – e di due lampadine, una con luce rossa R e una con luce verde V.

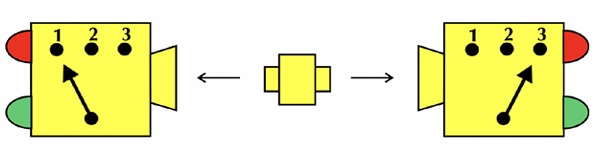
Supponiamo, inoltre, che il dispositivo possa rilevare particelle. Disponiamo due rilevatori come in figura: al centro c’è un dispositivo che emette due particelle in uno stato entangled, una verso il rilevatore A di sinistra, l’altra verso il rilevatore B di destra. Ogni volta che una particella viene intercettata da un rilevatore di Mermin, una delle due lampadine si accende ma mai entrambe contemporaneamente. Immaginiamo che i due rilevatori A e B siano indipendenti fra loro e che non possano comunicare. Immaginiamo anche che durante l’esperimento gli interruttori dei due rilevatori siano spostati a caso. Denotiamo lo stato di questi interruttori con la coppia di posizioni che possono occupare: per esempio lo stato A1B2 indica che il rilevatore A ha l’interruttore posizionato su 1 e il rilevatore B ha l’interruttore posizionato su 2. Lo stato A3B3 indica che entrambi i rilevatori hanno gli interruttori posizionati su 3. E così via. Ora, quel che accade conducendo l’esperimento è che, se gli interruttori sono sulla stessa posizione (stati A1B1, A2B2 o A3B3), allora le luci di entrambi i rilevatori sono dello stesso colore (entrambe rosse o entrambe verdi). Altrimenti, le luci sono dello stesso colore una volta su quattro: esiste cioè il 25% di probabilità che lo siano. Questo è quel che realmente accade nell’esperimento di Aspect: 25% è un valore sperimentale!
Possiamo comporre una tabella, come quella in questa pagina che contiene tutte le possibili combinazioni dei due interruttori e le corrispondenti probabilità che nei due rilevatori si accendano luci dello stesso colore o di colori diversi.

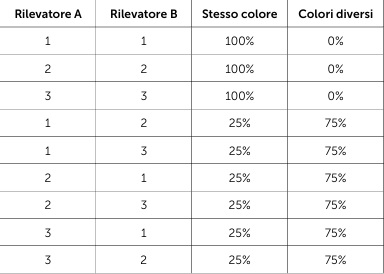
Non staremo a spiegare come sia possibile, ma si può realizzare un sistema quantistico, usando particelle in una sovrapposizione di stati, che soddisfa questa tabella in un esperimento reale. Invece, nella meccanica classica, non quantistica, questo è impossibile. Vediamo perché. Il caso in cui i due interruttori hanno la stessa posizione (A1B1, A2B2 o A3B3) è facilmente realizzabile anche con sistemi non quantistici: basta emettere due particelle identiche nelle due direzioni opposte e progettare il rilevatore in modo che accenda una luce rossa o verde a seconda di una caratteristica della particella, per esempio la velocità: se sono emesse alla stessa velocità, chiaramente i due rilevatori accenderanno la stessa lampadina in questo caso.
Dunque, supponiamo che le due particelle siano emesse avendo lo stesso valore di una loro grandezza fisica misurata dai due rilevatori: questa grandezza fisica non è quantistica e quindi ha uno stato definito, non può essere in una sovrapposizione di stati. Poiché un rilevatore di Mermin ha l’interruttore che, a un dato istante, sta in uno dei tre stati (1,2,3), possiamo caratterizzare la grandezza fisica misurata dal rilevatore in termini di una terna di valori (x,y,z) che possono assume re i valori R o V a seconda che facciano accendere la luce rossa o verde nel rilevatore in una delle tre rispettive posizioni dell’interruttore. Per esempio, la terna (R,R,R) corrisponde a una grandezza fisica che fa sempre accendere la luce rossa, la terna (R,R,V) corrisponde a una grandezza fisica che fa accendere la luce rossa se l’interruttore sta nelle posizioni 1 o 2 e la luce verde se sta nella posizione 3, (R,V,V) corrisponde a una grandezza fisica che fa accendere la luce rossa se l’interruttore sta nella posizione 1 e la luce verde se sta nelle posizioni 2 o 3 ecc. A conti fatti, abbiamo otto possibili terne: (R,R,R), (R,R,V), (R,V,R), (R,V,V), (V,R,R), (V,R,V), (V,V,R), (V,V,V).
Torniamo ora alla tabella precedente: abbiamo nove combinazioni possibili di posizioni degli interruttori di A e B. Nei casi A1B1, A2B2 e A3B3, quale che sia la terna che caratterizza la proprietà rilevata dal rilevatore, la probabilità che la stessa luce si accenda è banalmente del 100%. Nei rimanenti sei casi (cioè A1B2, A1B3, A2B1, A2B3, A3B1 e A3B2), la prima terna (R,R,V) accende la stessa luce solo nei casi A1B2 e A2B1; la seconda terna (R,V,R) accende la stessa luce solo nei casi A1B3 e A3B1; la terza terna (R,V,V) accende la stessa luce solo nei casi A2B3 e A3B2 e così via. Ciascuna terna accende la stessa luce solo in 2 casi su 6, cioè nel 33% dei casi. Pertanto, non è possibile realizzare un sistema di particelle classiche che possa soddisfare la tabella precedente, con quel 25% che invece è sperimentalmente verificato per sistemi di particelle come i fotoni.
Ecco perché il mondo è quantistico.