146. Giochi del 7 aprile 2025 – Il sogno di un quadrato

I Giochi del Lunedì di Prisma del 7 aprile 2025 a cura di Fabio Ciuffoli 

Oggi proponiamo un paio di problemi che prendono spunto dalle vicende di uno stravagante quadrato, dai suoi sogni, dalla nostra immaginazione e da altre geometrie. Ci piacerebbe pensarli come l’inizio di un breve racconto matematico di genere fantastico… Invitiamo i lettori a inviarci suggerimenti, racconti simili, osservazioni e proposte di soluzione utilizzando lo spazio dei  commenti. Domani alle ore 17.00 pubblicheremo le  nostre proposte di soluzione.

Il sogno di un quadrato

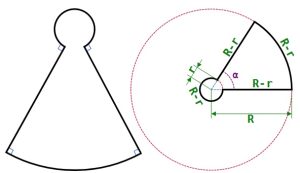
1. Nel mondo dei sogni, il tempo e lo spazio si dilatano e si contraggono creando spesso assurde distorsioni che la ragione fatica a comprende. E così un quadrato, pensato come un ipotetico abitante di Flatlandia, sogna di trasformarsi, di diventare flessibile, di contorcersi e di distorcersi con i suoi 4 lati della stessa lunghezza e i suoi 4 angoli retti, nulla di più e nulla di meno. Nella figura, a sinistra, vedete come si presenta in pubblico e a destra come si sente dentro di sé. Ecco la domanda: se tale figura esistesse, quanto misurerebbe l’angolo alfa? E in questa sua nuova forma a “buco di serratura” di quanto sarebbe variata l’area in percentuale rispetto all’area del quadrato di origine?

2. In questo secondo problema il nostro stravagante quadrato va a mapparsi su un’ideale sfera terrestre, come illustrato in figura. La lunghezza di ciascuna linea deve essere la stessa, gli angoli devono essere gli stessi, i lati devono essere dritti e paralleli. Si inizia dall’equatore (1), poi si viaggia verso nord lungo la linea gialla e dopo n miglia si raggiunge (2) quindi si svolta di 90 gradi a sinistra verso ovest lungo la linea blu. Dopo aver viaggiato per n miglia attorno alla parte posteriore della sfera fino a (3) si gira di 90 gradi a sinistra e si viaggia verso sud lungo la linea rossa. E dopo n miglia si raggiunge (4) poi si svolta di 90 gradi a destra verso ovest lungo la linea verde, tornando così al punto di partenza.

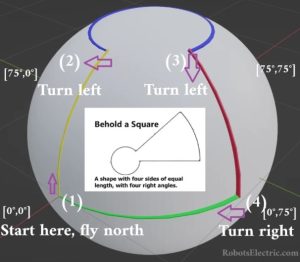
In questo sistema di coordinate, il segmento della linea verde è parallelo al segmento della linea blu (stessi valori di latitudine, rettilineo est-ovest). Il segmento della linea gialla è parallelo al segmento della linea rossa (stessi valori di longitudine, dritto nord-sud). Per un certo valore di n, si torna al punto di partenza, completando il “quadrato”.

Qual è il valore di n? E quali sono le coordinate degli angoli?

Aggiornamento per le soluzioni click qui.

Il primo problema nasce ad una suggestione dall’ottimo sito web Base5 curato da Gianfranco Bo, che ringraziamo per la disponibilità e la collaborazione. https://utenti.quipo.it/base5/diario2024.html

Il secondo problema, con la relativa soluzione, è tratto dal sito reddit.com un interessante sito di social news specializzato. https://www.reddit.com/r/mathmemes/comments/1fk15k3/behold_a_square/