140. Soluzioni del 13 gennaio 2025 – Matematica dall’Ungheria
Nessun commento
Menu
Soluzioni del 13 gennaio 2025 a cura di Fabio Ciuffoli
Ieri abbiamo presentato quattro problemi tratti da una recente prova di matematica (Dürer Math Competition) per ragazzi ungheresi di età tra i 14 e i 16 anni. Di seguito pubblichiamo le soluzioni commentate.
Matematica dall’Ungheria
1. Piantare papaveri. Morfeo, il dio dei sogni, ha un giardino quadrato ABCD di lato 30 metri. Vuole piantare il papavero nell’ottagono definito dai punti di trisezione EFGHIJKL. Qual è l’area di questo ottagono in metri quadrati?
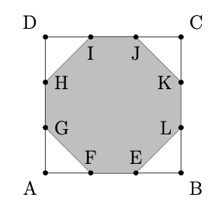
1. SOLUZIONE. Ci sono diversi modi per risolvere questo problema. Possiamo sottrarre dall’area di ABCD, le aree di 4 triangoli rettangoli isosceli che hanno i cateti lunghi 10 m. L’area totale di questi triangoli è AT = 4 • (102/2) = 200 m2. L’area del quadrato ABCD è AQ = 302 = 900 m2. Infine l’area dell’ottagono è AO = AQ – AT = 900 – 200 = 700 m2.
2. L’esercito di Ares. Ares è a capo di un esercito composto da Centauri, Uomini e Cavalli Alati. Ognuno ha 1 testa, i Centauri e i Cavalli Alati hanno 4 gambe, gli Uomini hanno 2 gambe, mentre i Centauri e gli Uomini hanno 2 braccia, mentre i Cavalli Alati non hanno braccia. Sapendo che ci sono 193 teste, 666 gambe e 244 braccia, quanti Centauri fanno parte dell’esercito di Ares?
2. SOLUZIONE. Indichiamo con U gli Uomini, con Ca i Cavalli Alati e con Ce i Centauri, possiamo scrivere il problema:
Moltiplichiamo per 4 la prima equazione e sottraiamo la seconda equazione dalla prima, avremo:
Ora, sostituendo nella U terza equazione, calcoliamo il numero dei Centauri:
2Ce = 244 – 106 = 138 quindi Ce = 138/2 = 69.
Infine dalla prima equazione ricaviamo il numero dei Cavalli Alati = 193 – 53 – 69 = 71.
3. Tessere Testa d’Ascia. I bordi di queste tessere identiche sono quarti di cerchio e i loro centri sono i punti contrassegnati. Determinare l’area di una piastrella, misurata in cm2, sapendo che l’altezza di una piastrella, tratteggiata in figura, è 12 cm.
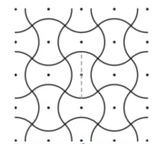
3. Soluzione. La parte superiore di una piastrella in piedi è un quarto di cerchio, il cui centro è il centro della piastrella, quindi il raggio del quarto di cerchio è 6 cm e anche gli angoli della piastrella sono a 6 cm dal centro della piastrella come mostrato in figura.
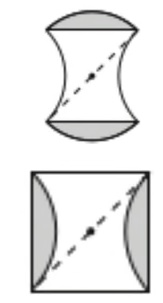
Possiamo sezionare la tessera rimuovendo i segmenti circolari in alto e in basso e posizionandoli nei posti vuoti sui lati sinistro e destro della tessera. Otteniamo così un quadrato con una diagonale di 12 cm. Indichiamo con s la lunghezza del lato del quadrato e per il Teorema di Pitagora avremo: s2 + s2 = 122 che diviene 2s2 = 144. Infine l’area del quadrato è s2 = 144/2 = 72 cm2.
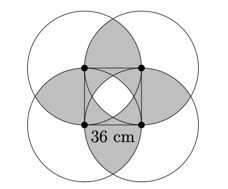
4. SOLUZIONE. L’area ombreggiata si può scomporre in quattro parti congruenti di cui una è disegnata in figura seguente. Infatti se spostiamo questa parte a sinistra, la ruotiamo di 90 gradi in senso orario e ripetiamo l’operazione per tre volte, otteniamo l’area totale ombreggiata.
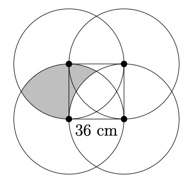
Ora spostiamo la ‘squama di pesce’ a sinistra del quadrato e, dopo averla ruotata di 90 gradi in senso orario, la inseriamo all’interno del quadrato, come mostrato in figura seguente.
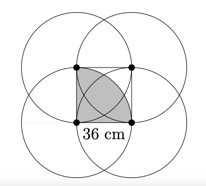
Otteniamo così un quarto di cerchio di raggio 36 cm. Ora l’area totale della parte ombreggiata è quattro volte l’area del quarto di cerchio, quindi (36 • 36)π = 1.296π = 4.069,44 cm2.
I Giochi del Lunedì tornano tra due settimane.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).