
Soluzioni del 21 ottobre 2024 a cura di Fabio Ciuffoli
Ieri abbiamo presentiamo tre problemi di matematica applicata, tratti dalla rivista New Scientis e di seguito pubblichiamo le soluzioni.
Fiori, grattacieli e banchine – soluzioni
1. Il deposito di fiori. Le strade di una città sono disposte secondo una griglia rettangolare come disegnato in figura.
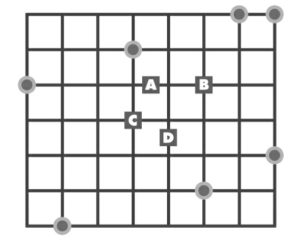
Sette fiorai, indicati dai cerchi, gestiscono le loro bancarelle nelle stazioni della metropolitana e vogliono allestire un deposito centrale da dove poter ritirare i fiori ogni mattina. Vogliono mantenere al minimo la distanza combinata dalle bancarelle al deposito. Paolo ha selezionato quattro luoghi possibili: A, B, C e D. Sandro chiede: “Sei sicuro che una di queste quattro sia la posizione ottimale? Suppongo che dovremmo verificare la distanza totale fioraio-deposito per ogni punto della griglia”. Interviene Carla: “Non è necessario, posso dirti con sicurezza la posizione migliore semplicemente guardando il diagramma”. Quale luogo consiglia Carla e perché è così sicura?
1. SOLUZIONE. La posizione con la distanza combinata minima è B. Supponiamo che il deposito sia allineato con il quarto venditore da sinistra. Se il deposito venisse spostato a sinistra, la distanza dei tre venditori a sinistra si ridurrà, ma la distanza dei quattro venditori a destra aumenterà, quindi la distanza combinata complessiva sinistra-destra aumenterà. Allo stesso modo, se si allinea il deposito con il quarto venditore dall’alto, qualsiasi cambiamento nella coordinata verticale aumenterà la distanza totale. Carla ha capito che il deposito dovrà trovarsi nella posizione orizzontale e verticale dei venditori centrali, in quelle due direzioni, ovvero B.
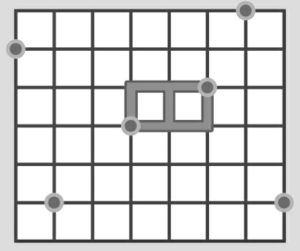
Questo problema di ottimizzazione è un adattamento di un vecchio enigma. In una versione risalente a 40 anni fa o più, la soluzione prevedeva che il posizionamento ottimale si raggiungesse attraverso una serie di voti: ai venditori sarebbe stato chiesto se volevano che il deposito fosse spostato a nord, sud, est o ovest. Si tratta tuttavia di una strategia prolissa e forse un po’ irrealistica. Vale la pena sottolineare che la posizione ottimale del deposito non è sempre un unico punto. Affinché la posizione sia un unico punto è necessario che vi sia un numero dispari di venditori. Infatti con sei venditori, se li dividiamo in gruppi di tre est/ovest, c’è una zona in cui muoversi in entrambe le direzioni non fa alcuna differenza sulla distanza totale. Allo stesso modo con nord/sud. In questo caso, la posizione ottimale del deposito sarà una regione anziché un punto, come mostrato nella figura di seguito. Il deposito può essere posizionato ovunque sulle linee più larghe mostrate e la distanza totale di consegna sarà la stessa.
2. L’elettricista. Un alto grattacielo viene ricablato. Ci sono quattro fili che entrano in un tubo e vanno dal piano terra all’ultimo piano. I fili sono assolutamente identici, è impossibile districarli e distinguerli. L’elettricista ha pensato a un modo per individuarli: inizia dal piano terra, collegando due fili insieme (ad esempio A e C) poi si reca all’ultimo piano a piedi, perché l’ascensore è fuori uso, e mediante un tester (strumento che rileva i collegamenti tra i cavi) prova quali sono i due fili che formano un circuito elettrico, ad esempio 1 e 3. Qual è il numero minimo di salite e discese delle scale, che l’elettricista dovrà compiere per contrassegnare correttamente i quattro i cavi?

2. SOLUZIONE. Sono necessarie una salita e una discesa delle scale. L’elettricista collega prima A con B (I) e poi si reca all’ultimo piano e utilizzando il tester trova i fili che formano il circuito e li collega, ipotizziamo che siano 2 e 4 (II) come illustrato in figura.
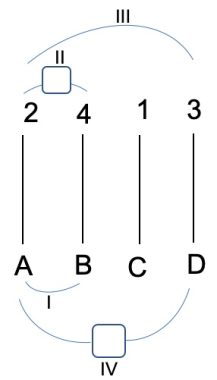
A questo punto collega un cavo di quella coppia a un altro cavo inutilizzato, ipotizziamo 2 con 3 (III) e torna a piano terra. Qui disconnette A e B e di nuovo cerca la coppia che forma un circuito. Una di queste sarà A o B (l’altra estremità di 2), l’altra sarà C o D (l’altra estremità di 3). Supponiamo che trovi collegati A con D (IV). Ora ha tutte le informazioni: A è 2, quindi B è 4, D è 3 e per esclusione C deve essere 1.
3. La barca in porto. Una barca viene legata tramite una corda a una banchina e quando la corda è tesa la barca dista 1 metro dalla banchina, come disegnato in figura. E’ in arrivo una tempesta e il marinaio, nel tentativo di evitare l’urto tra la barca e la banchina, decide di tirare la corda orizzontalmente di un metro, perciò la barca si muoverà orizzontalmente. La barca raggiungerà la banchina oppure no?
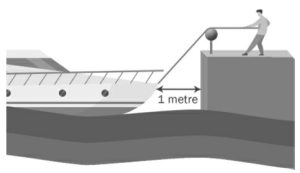
3. SOLUZIONE. Se il marinaio tira la corda orizzontalmente di un metro, la barca non solo raggiungerà la banchina ma si scontrerà con il muro.
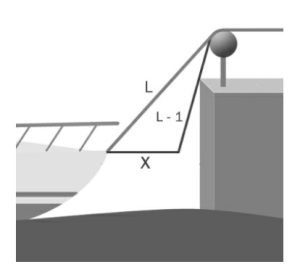
Supponiamo che la barca si avvicini di una distanza X, come illustrato in figura. La corda tesa di lunghezza L viene accorciata di un metro per diventare L − 1. La somma dei due lati più corti del triangolo deve essere maggiore del lato più lungo (questa è una regola di tutti i triangoli). Quindi X + L − 1 > L, da cui X − 1 > 0 infine X > 1. La maggior parte delle persone trova questa risposta sorprendente. Anche gli insegnanti di matematica e gli accademici tendono a sbagliare. Ha qualcosa a che fare con la trazione orizzontale della corda che si trasforma in una trazione diagonale, dando l’impressione che venga utilizzata solo una parte del movimento orizzontale. E’ stato rilevato che le persone con una solida conoscenza matematica, tendono ad attingere ai concetti più avanzati e iniziano a disegnare diagrammi, svolgere calcoli e impostare equazioni trigonometriche, mentre l‘esperienza fisica può migliorare l’intuizione. Chiunque abbia familiarità con l’ormeggio di una barca si renderà conto che trainare la barca verso un molo è un lavoro estremamente faticoso se la corda è inclinata, infatti per ogni metro di corda tirato, la barca percorre più di un metro!
I Giochi del Lunedì tornano tra due settimane.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).