In un’arguta barzelletta, un fisico e un economista dimostrano che tutti i numeri dispari maggiori di 1 sono numeri primi (enunciato evidentemente falso). Il fisico dice: «3 è primo, 5 è primo, 7 è primo, 9 è un errore di misurazione, 11 è primo, 13 è primo… dai, sono tutti primi». L’economista dice: «3 è primo, 5 è primo, 7 è primo, 9 è primo, 11 è primo, 13 è primo… dai, sono tutti primi». Frecciatine a parte, spesso tutti siamo tentati di ragionare in modo empirico e approssimativo, traendo conclusioni generali da un campione ridotto. La barzelletta quindi è anche istruttiva: mostra che, se vogliamo studiare in modo accurato un caso generale, non possiamo fermarci a guardare quello che succede con i numeri piccoli. Ci sono anzi diversi esempi di successioni numeriche che all’inizio sembrano elementari e invece sono ingannevoli. Consideriamo una sequenza facile: 1, 2, 3, 4. Cosa viene dopo? La risposta ovvia è 5. Ma c’è almeno un’altra possibile risposta. A entrare in gioco sono i numeri perfetti, cioè quelli uguali alla somma dei propri divisori: per esempio 6(=1+2+3) e 28 (=1+2+4+7+14). I più piccoli numeri perfetti conosciuti sono 6, 28, 496, 8.128, 33.550.336. Se contiamo il numero delle loro cifre, otteniamo la sequenza 1, 2, 3, 4, 8. Questo non vuol dire che la risposta “5” sia necessariamente sbagliata a priori; solo, non è l’unica possibile risposta giusta. Se un fisico si trovasse di fronte a un fenomeno naturale i cui primi dati sono {1, 2, 3, 4}, non potrebbe arrivare a concludere che la legge matematica che lo governa è la successione dei numeri naturali, perché ce n’è almeno un’altra. Una sequenza che sembra ancora più elementare è 1, 1, 1, 1. Si è portati a pensare che continui così all’infinito, ma in questo caso al quinto posto potremmo far comparire un 2. Pensiamo al triangolo di Tartaglia – quello che si studia a scuola – in cui ogni elemento è la somma dei due che gli stanno sopra:
Se si leggono i numeri del triangolo secondo le righe, la successione che si ottiene è 1,1,1,1,2,1, 1, 3, 3, 1, 1, 4, 6, 4, 1, … Ma torniamo ai numeri primi: data la sequenza 2, 3, 5, 7, 11, 13, quale numero viene dopo? È intuitivo pensare immediatamente a 17. E invece no. Consideriamo le frazioni, in particolare quelle semplificate e in cui il numeratore è minore o uguale al denominatore (cioè quelle della forma 2/3, 3/5, ecc.). Prendiamo al primo passo quelle che al denominatore hanno 1: sono solo 0/1 e 1/1 (due in tutto). Quelle con denominatore minore o uguale a 2 sono 0/1, 1/2, e 1/1 (tre in tutto). Al terzo passo (quelle con denominatore minore o uguale a 3) abbiamo 5 frazioni: 0/1, 1/3, 1/2, 2/3 e 1/1. E così via: al quarto passo sono 7 (0/1, 1/4, 1/3, 1/2, 3/4, 2/3, 1/1), al quinto sono 11 (0/1, 1/5, 1/4, 1/3, 1/2, 2/5, 3/5, 4/5, 3/4, 2/3, 1/1) e al sesto 13 (0/1, 1/6, 1/5, 1/4, 1/3, 1/2, 5/6, 2/5, 3/5, 4/5, 3/4, 2/3, 1/1). Ecco quindi la sequenza dei primi sei termini: 2, 3, 5, 7, 11, 13. Solo che al settimo passo le frazioni sono 19: 0/1, 1/7, 1/6, 1/5, 1/4, 1/3, 1/2, 2/7, 3/7, 4/7, 5/7, 6/7, 5/6, 2/5, 3/5, 4/5, 3/4, 2/3, 1/1. Il settimo numero della successione quindi non è 17 ma 19. Ancora: esaminiamo la sequenza 1, 2, 4, 8, 16. Il numero successivo è 32? Non necessariamente, però stavolta ci si va molto vicino. Consideriamo la sequenza ottenuta prendendo su una circonferenza prima un punto, poi due, poi tre e così via. E ogni volta colleghiamo tra loro tutti i punti (figura 1).
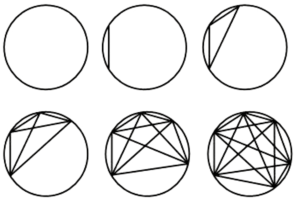
In quante parti viene diviso il cerchio? Con un punto non ci sono segmenti e resta una parte sola, con due punti c’è un segmento e quindi due parti, con tre punti tre segmenti e 4 parti e così via: la sequenza è 1, 2, 4, 8, 16, 31. Contare per credere.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
Una risposta
Concordo e segnalo il progetto On-Line Encyclopedia of Integer Sequences (OEIS -https://oeis.org/), un mastodontico database che raccoglie ad oggi 374034 sequenze di interi. Il progetto di raccolta e catalogazione è stato iniziato nel 1964 dall’allora studente Neil Sloane e oggi, gestito da una apposita fondazione, è il riferimento più autorevole e completo per il settore delle successione di interi, e si arricchisce di circa 30 sequenze ogni giorno. Se non riuscite a venire a capo di una sequenza di interi, inserite i primi elementi nella barra di ricerca e l’archivio vi dirà quali sequenze iniziano con quei termini, corredate di riferimenti matematici e altre sequenze correlate.
Buon lavoro.