131. Soluzioni del 9 settembre 2024 – Test d’ingresso per la scuola media in Giappone

Soluzioni del 9 settembre 2024 a cura di Fabio Ciuffoli

Ieri abbiamo presentato quattro problemi tratti dalle prove d’ingresso alle scuole medie private giapponesi per alunni di 12 anni. Di seguito pubblichiamo le nostre proposte di soluzione tenendo conto delle competenze medie di un ragazzo di 12 anni. 

Test d’ingresso per la scuola media in Giappone – soluzioni 

1. Tre quadrati

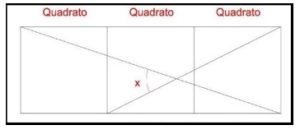
Determinare l’ampiezza dell’angolo x.

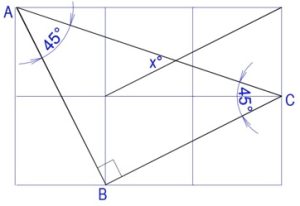
1. SOLUZIONE. Si disegnano i tre quadrati sottostanti, come in figura e si tracciano i segmenti AB e BC. L’angolo ABC è retto e il triangolo ABC è rettangolo isoscele con i due angoli uguali di 45°. BC è parallelo al segmento che forma l’angolo x, per cui x = 45 gradi.

2. Quadrato e cerchio.

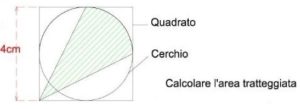
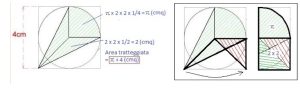
2. SOLUZIONE. L’area tratteggiata è composta da un quarto di cerchio più due triangoli uguali di base 2 cm e altezza 2 cm. Nella figura seguente a destra la soluzione algebrica e a sinistra la  soluzione mediante scomposizione.

3. Un quadrato e due triangoli.

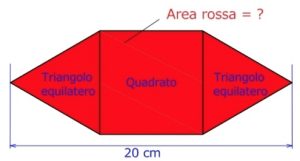
3. SOLUZIONE. Utilizzando i simboli in figura abbiamo (a + 2b) = 20 cm che diviene (a/2 + b) = 10.  Procediamo alla scomposizione della figura disegnando il quadrato ABCD che avrà lato (a/2 + b) = 10 cm. Ora, spostiamo i due triangoli rettangoli seguendo le frecce verdi così vedremo che l’area rossa è uguale a quella del quadrato ABCD = 10 • 10 = 100 cm².

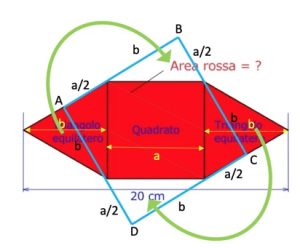
Procedimento algebrico. Utilizzando le formule del triangolo equilatero per cui l’altezza h = l√3/2 quindi  l√3/2 + l + l√3/2 = 20

che diviene l√3 + l = 20

raccogliendo l(1 + √3) = 20

quindi l = 20/(1 + √3)

Ora, elevando al quadrato  l² = 400/(4 + 2√3) semplificando otteniamo

(1) l² = 100/(1 + √3/2).

Utilizzando le formule dell’area del triangolo equilatero, conoscendo il lato,  A = l²√3/4.

L’area rossa è data dalla somma dell’area del quadrato e dall’area dei due triangoli equilateri, quindi A_rossa = l² + 2l²√3/4 semplificato = l² + l²√3/2. Ora raccogliendo avremo A_rossa = l²(1 + √3/2) infine sostituendo l² con la (1) avremo A_rossa = [100/(1 + √3/2)] (1 + √3/2) che si semplifica quindi A_rossa = 100 cm².

4. Un quadrato con un triangolo rosso.

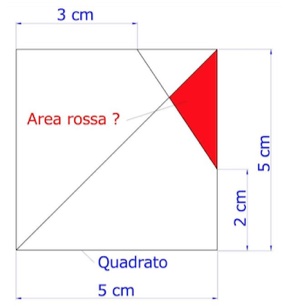
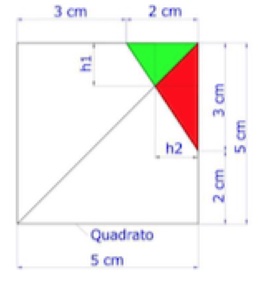
4. SOLUZIONE. Completiamo il disegno con il triangolo verde e inserendo le misure, come in figura. Il triangolo verde ha area 2h₁/2 = h₁. Il triangolo rosso ha area 3h₂/2. Il triangolo rettangolo, composto dai due triangoli verde e rosso, ha area 2•3/2= 3 cm². Essendo h₁ = h₂, il rapporto tra l’area dei triangolo rosso e l’area del triangolo verde è 3/2, quindi il triangolo rosso è 3/5 dell’area del triangolo rettangolo. Infine l’area del triangolo rosso è 3•3/5 = 1,8 cm².

I Giochi del Lunedì tornano tra due settimane.