
I Giochi del Lunedì di Prisma del 9 settembre 2024 a cura di Fabio Ciuffoli
I quattro problemi che presentiamo oggi sono tratti dalle prove d’ingresso alle scuole medie private giapponesi per alunni di 12 anni. In Giappone nella scuola elementare si fanno molti esercizi di “pensiero laterale” e di immaginazione spaziale e perciò i ragazzi sono abituati a questa tipologia di test, mentre per un adulto non sempre risultano facili. Le soluzioni sono sorprendentemente semplici, non occorrono equazioni, radici quadrate e trigonometria, ma un po’ di fantasia e creatività. Invitiamo i lettori a inviarci osservazioni e proposte di soluzione utilizzando lo spazio riservato ai commenti. Domani alle ore 17.00 pubblicheremo le soluzioni.
Aggiornamento per le soluzioni click qui.
Test d’ingresso per la scuola media in Giappone
1. Tre quadrati
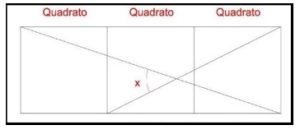
Determinare l’ampiezza dell’angolo x.
2. Quadrato e cerchio.
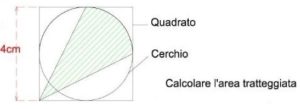
3. Un quadrato e due triangoli.
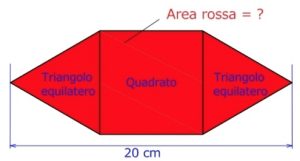
4. Un quadrato con un triangolo rosso.
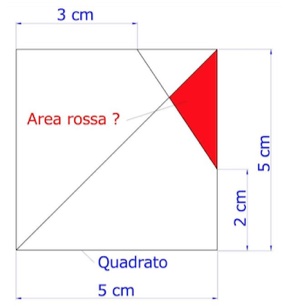
I problemi sono tratti dalle prove d’ingresso per le scuole medie private in Giappone. Ringraziamo Masahiro Matsuno, architetto e appassionato di logica e matematica, per la condivisione.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
23 risposte
N. 4
A e B hanno la stessa altezza, quindi:
2A = 3B
A+B = 3
da cui A = 9/5 cmq, B = 6/5 cmq.
Problema 1 via trigonometrica
Ottimo grazie per la condivisione. Nel pomeriggio le soluzioni commentate.
Problema 4
Problema 3
Problema 1
2. vedi allegato
Problema 4.
Per la geometria del quaderno a quadretti: se prolungo il lato obliquo inferiore del triangolo rosso, incontrerà il prolungamento del lato sinistro del quadrato in un punto a un’altezza 9/2 sopra al lato superiore del quadrato. Sfruttando poi la similitudine del triangolo rosso con quello formato da questi prolungamenti, detta h l’altezza del triangolo rosso, ho:
(5+9/2) : 3 = (5-h) : h
Applicando la proprietà del comporre risolvo la proporzione e ottengo h = 6/5
da cui l’area cercata e’ 1/2 * 3 * 6/5 = 9/5
[ niente trigonometria, niente software, niente radici quadrate, niente Pitagora/Euclide, solo similitudini e proporzioni ]
2. Vedi immagine
Problema 4 – vedi allegato
Ti ringrazio Fabio della pubblicazione. Questi sono gli esempi più significativi del “Lateral thinking”.
Inviterei tutti a provare la soluzione dei quesiti e allegare un disegno dimostrativo (anche un semplice schizzo). Un altro tema didattico importante è il pragmatismo (cioè comunicare il tuo pensiero con la massima efficacia) spesso un disegno parla più di mille parole. Buon divertimento.
3. vedi immagine
Problema 1 – soluzione geometrica e trigonometrica. vedi allegati
soluzione trigonometrica
Problema 4.
Analizzando i due triangolini (quello rosso e quello bianco), si può notare che le loro altezze (relative alle basi sui lati del quadrato) sono uguali, partendo appunto dalla diagonale del quadrato.
Questa altezza si ricava dalla relazione:
A(rosso) + A(bianco) = A(triangolo rettangolo al vertice)
3*h/2 + 2*h/2 = 3*2/2
da cui: h = 1,2
Quindi l’area del triangolino rosso è:
A(rosso)= 1,8
A domani per le soluzioni commentate.
Seguendo l’ottimo consiglio del dott. Matsuno, aggiungo immagine esplicativa alla mia risoluzione:
Problema 2.
Indichiamo con
AQ: Area del Quadrato = 16
AC: Area del Cerchio = 4*pigreco
L’area richiesta sarà:
A = AQ – 2/4AQ – 1/4(AQ-AC) = 1/4AQ + 1/4AC
Quindi: A = 4 + pigreco
Allego immagine:
Problema 3.
Ricomponendo opportunamente la figura (si tagliano i triangoli e si ricompongono in rettangoli), si calcola con semplici passaggi che l’area totale rossa = 100
Problema 1 – L’angolo richiesto è la somma degli angoli che i due segmenti obliqui formano con i lati orizzontali dei quadrati. Nel caso del segmento 3×1 l’angolo è arctan(1/3), nel caso del segmento 2×1 l’angolo è arctan(1/2), quindi l’angolo richiestoè arctan(((1/3)+(1/2))/(1-(1/2)(1/3)))=arctan(1)=45°
Aggiungiamo una fila di quadrati sotto quella disegnata, trasliamo il segmento 2×1 di 1 verso il basso e poi disegniamo un segmento 1×2 da vertice in alto a sinistra del rettangolo 3×2 fino all’estremità destra del segmento 2×1. In tal modo si forma un triangolo isoscele i cui angoli alla base sono uguali a x per parallelismo. Il triangolo isoscele in questione è anche rettangolo perché i due segmentui 2×1 e 1×2 sono tra loro perpendicolari: nel punto in cui incontrano ci sono tre angoli che assommano un piatto di cui due sono angoli interni di traingoli rettangoli uguali.
Essendo un triangolo rettangolo isoscele x=45°
Vedi immagine allegata