
Le soluzioni del 15 luglio 2024 a cura di Fabio Ciuffoli
Ieri abbiamo presentato due problemi sull’istinto matematico degli animali e di seguito pubblichiamo le nostre proposte di soluzione.
L’istinto matematico – soluzioni
1. Il cane all’inseguimento della pallina Un cane e il suo padrone stanno giocando sulla riva di un lago. Il padrone lancia una pallina nell’acqua ed il cane va a recuperarla. Se il lancio è dritto davanti a sé, il cane si butta nel lago e nuota direttamente verso la pallina. Se il lancio è in diagonale, rispetto al punto dove si trova il cane sulla spiaggia, allora il cane, invece di buttarsi direttamente verso la pallina, corre lungo la riva per un po’ prima di tuffarsi in acqua e poi nuotare fino alla pallina. Il cane vuole recuperare la pallina nel minor tempo possibile. Dal momento che esso può muoversi molto più velocemente sulla terraferma di quanto lo possa fare nuotando in acqua, la via più veloce è correre lungo la riva per un tratto e poi tuffarsi e nuotare per il tratto rimanente.
Schematizzando, con il disegno in figura, la pallina lanciata si trova in B e il cane in A. Il cane corre lungo la riva fino al punto D e poi si getta in acqua e nuota in direzione di B. Supponiamo che BC sia 10 metri, AC sia 20 metri e che la velocità del cane a terra sia 4 volte maggiore della sua velocità in acqua, si chiede di calcolare la distanza AD che il cane percorre a riva prima di tuffarsi in acqua al fine di minimizzare il tempo per raggiungere B?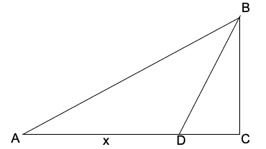 1. SOLUZIONE. Il minor tempo, in cui il cane può raggiungere la pallina, è dato dal percorso AD più DB. Indichiamo con x la distanza AD percorsa dal cane lungo la riva. Utilizzando il teorema di Pitagora, il tempo di percorrenza sarà espresso dalla seguente funzione f(x) = (1/4)x + √[102 + (20 – x)2]. La frazione ¼ indica che la velocità del cane a terra è 4 volte maggiore rispetto alla sua velocità in acqua. Svolgendo avremo (1/4)x + √(x2 – 40x + 500). Possiamo procedere in modo empirico, sostituendo x per tentativi con valori tra zero e 20 e calcolare il minimo tempo di percorrenza, come proposto in tabella, oppure calcolare il minimo con la derivata della funzione con risultato 17,42.
1. SOLUZIONE. Il minor tempo, in cui il cane può raggiungere la pallina, è dato dal percorso AD più DB. Indichiamo con x la distanza AD percorsa dal cane lungo la riva. Utilizzando il teorema di Pitagora, il tempo di percorrenza sarà espresso dalla seguente funzione f(x) = (1/4)x + √[102 + (20 – x)2]. La frazione ¼ indica che la velocità del cane a terra è 4 volte maggiore rispetto alla sua velocità in acqua. Svolgendo avremo (1/4)x + √(x2 – 40x + 500). Possiamo procedere in modo empirico, sostituendo x per tentativi con valori tra zero e 20 e calcolare il minimo tempo di percorrenza, come proposto in tabella, oppure calcolare il minimo con la derivata della funzione con risultato 17,42. 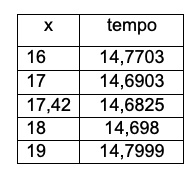 La lunghezza AD misura 17,42 metri.
La lunghezza AD misura 17,42 metri.
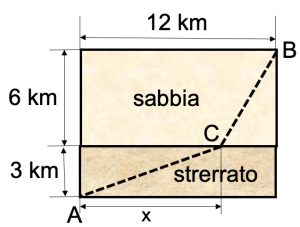
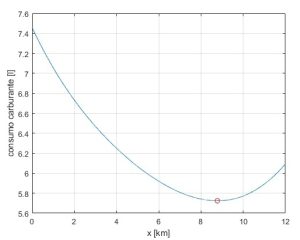
2. Strada sterrata o sabbiosa. Un’automobile fuoristrada deve andare dal punto A al punto B con le distanze rappresentate in figura. Deve attraversare, inizialmente, un tratto sterrato con un consumo di carburante 0,25 litri al km e poi un tratto sabbioso con consumo di carburante 0,5 litri al km. Individuare il percorso che minimizza il consumo di carburante e calcolare il consumo totale di carburante.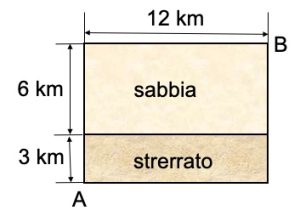 2. SOLUZIONE. Per avere il minimo consumo di carburante è necessario seguire un percorso a spezzata formato dai tratti AC e CB, che sono le due ipotenuse dei triangoli rettangoli, illustrati in figura. Per individuare il punto C, indichiamo con x i kilometri del cateto del triangolo con ipotenusa AC e otteniamo la seguente funzione di consumo del carburante f(x) = 0,25(√(x2+ 32) + 0,5√[(12 – x)2 + 62] della quale riproduciamo il grafico. Derivando, si ottiene il minimo per x = 8,777747662 km. Ora calcoliamo il consumo di carburante andando a sostituire x nella funzione di consumo e avremo 5,724313 litri. Diverse soluzioni proposte dai partecipanti sono molto dettagliate e precise, alcune indicano anche le distanza AC e CB. Un ottimo lavoro, ringrazio i nostri bravissimi lettori.
2. SOLUZIONE. Per avere il minimo consumo di carburante è necessario seguire un percorso a spezzata formato dai tratti AC e CB, che sono le due ipotenuse dei triangoli rettangoli, illustrati in figura. Per individuare il punto C, indichiamo con x i kilometri del cateto del triangolo con ipotenusa AC e otteniamo la seguente funzione di consumo del carburante f(x) = 0,25(√(x2+ 32) + 0,5√[(12 – x)2 + 62] della quale riproduciamo il grafico. Derivando, si ottiene il minimo per x = 8,777747662 km. Ora calcoliamo il consumo di carburante andando a sostituire x nella funzione di consumo e avremo 5,724313 litri. Diverse soluzioni proposte dai partecipanti sono molto dettagliate e precise, alcune indicano anche le distanza AC e CB. Un ottimo lavoro, ringrazio i nostri bravissimi lettori.
I Giochi del Lunedì tornano tra due settimane.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).