La richiesta di prevenzione non è di parte

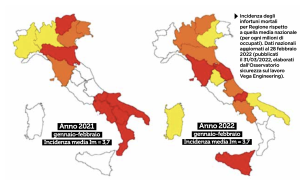
Provate a digitare, per chi ne ha la possibilità, “incidenti sul lavoro” negli archivi de Il Sole 24 ore e, per par condicio, in quelli de Il Manifesto. Solo tra l’1 gennaio e il 15 aprile di quest’anno la quantità di articoli pubblicati è imponente: 164.824 caratteri, 25.661 parole, 3.085 righe e 2.111 paragrafi. Tanto inchiostro riflette il fatto che nel primo bimestre del 2022 sono state 121.994 (+47,6% rispetto allo stesso periodo del 2021) le denunce di infortunio arrivate all’Inail, 114 delle quali con esito mortale (+9,6%). In aumento anche le patologie di origine professionale denunciate, che sono state 8.080 (+3,6%). Ne risulta la fotografia di un’Italia a colori, in cui sono rosse le regioni con un’incidenza infortunistica superiore al 125% di quella media nazionale, con un’intensità che degrada attraverso arancione e giallo fino al bianco che colora le regioni in cui l’incidenza è inferiore al 75% di quella media. Che cosa dicono, quali sono i termini maggiormente utilizzati e, soprattutto, quale chiave di lettura danno i due quotidiani di questo inaccettabile e pure incessante fenomeno?

Per rispondere a queste domande abbiamo fatto ricorso a un software per l’analisi testuale e alla matematica, che di per sé con gli infortuni sul lavoro c’entra fortunatamente ben poco. Programmi di questo tipo utilizzano strumenti matematici e statistici (oltre che, ovviamente, linguistici) per analizzare testi più o meno complessi e trasformarli in tabelle, elenchi, grafici e mappe che forniscono una sorta di “rappresentazione geometrica” che consente di leggerli da un punto di vista diverso. L’ipotesi alla base di un qualunque software per l’analisi testuale è la presenza di un legame profondo tra la struttura lessicale di un testo (cioè i lemmi più ricorrenti, le associazioni tra lemmi ecc.) e la sua dimensione semantica (cioè il significato che il testo vuole veicolare). Effettuare l’analisi di un testo con un programma di questo tipo ha senso se si crede che un’analisi mirata delle parole usate possa consentire di fare inferenze a proposito del messaggio che il testo stesso vuole trasmettere. Come funziona un software per l’analisi testuale? Per uno qualunque di questi programmi, il testo da analizzare non è altro che una lunga sequenza di parole, ciascuna delle quali non ha un senso in sé ma acquista un significato in base alle sue relazioni con le altre parole, cioè in base alla distribuzione delle sue occorrenze all’interno del corpus in esame. Di conseguenza, quando diamo in pasto a uno di questi software un testo più o meno lungo, questo viene innanzi tutto trasformato in un data base che codifica in maniera opportuna tutte le parole, contando quante volte e ricordando in che punto ognuna di loro compare all’interno del testo stesso. T-Lab, che è il software che abbiamo utilizzato per la nostra analisi, costruisce in prima battuta due elenchi: il primo è costituito da tutte le parole che compaiono nel testo (escluse congiunzioni, articoli ecc.) e il secondo da sottoinsiemi del testo, detti contesti elementari, che possono essere singole frasi, paragrafi o frammenti più o meno lunghi, determinati in base a criteri stabiliti dall’utilizzatore. Disponendo poi dei due elenchi, (p₁, p₂, … , p_n) e (c₁, c₂, … , c_m), e di una serie di tabelle allegate, che racchiudono tutte le informazioni rilevanti relative all’organizzazione del testo, il software è in grado di produrre, su richiesta dell’utente, matrici, elenchi, istogrammi, diagrammi a torta, grafici e mappe di vario genere. L’oggetto più immediato da descrivere è una grande matrice rettangolare, con n righe e m colonne: al posto ij T-Lab scrive il numero di volte che la parola p_i compare nel sottoinsieme c_j. In questo modo, ogni riga fornisce la distribuzione della parola corrispondente all’interno dei contesti in cui è frammentato il testo, mentre ogni colonna consente di stabilire quali parole compaiono, e quali no, nel corrispondente contesto elementare. Inoltre, dato l’elenco (p₁, p₂, … , p_n) delle parole, possiamo costruire un’altra matrice, detta matrice delle co-occorrenze, questa volta quadrata di ordine n, dove al posto ij troveremo il numero di contesti elementari in cui le parole p_i e p_j  compaiono insieme, ovvero il valore di co-occorrenza delle parole p_i  e p_j  nel testo. Supponiamo per esempio di avere un elenco di 6 parole, “lavoro”, “incidenti”, “operaio”, “sicurezza”, “cantiere” e “prevenzione”, considerate nell’ordine. Supponiamo poi di selezionare, tra tutti quelli scaricati, 10 articoli di uno dei due quotidiani, ciascuno dei quali costituisce un contesto elementare ed è quindi etichettato con un numero da 1 a 10. La prima matrice, quindi, sarà una matrice con 6 righe e 10 colonne, come la seguente:

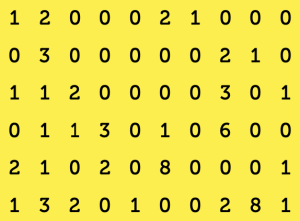
La prima riga fornisce la distribuzione della prima parola, lavoro, all’interno degli articoli selezionati: precisamente, lavoro compare una volta nel primo e nel settimo articolo, due volte nel secondo e nel sesto e mai nei restanti. La prima colonna, invece, fornisce l’elenco delle parole che compaiono nel primo articolo: vi si menzionano, dunque, lavoro, operaio, cantiere e prevenzione mentre non vi compare nessuna delle altre parole in esame. Analogamente possiamo interpretare le altre righe e colonne. Con lo stesso elenco di parole, e con i dati riassunti nella prima matrice, potete divertirvi a costruire da soli la matrice quadrata delle co-occorrenze, che sarà 6×6 e diagonale (perché?):

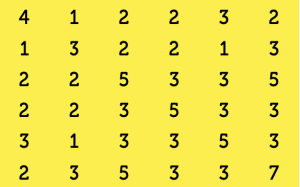
I numeri che appaiono sulla diagonale corrispondono al numero di articoli in cui appare la parola p_i. Tenete presente che l’esempio appena fatto è puramente teorico: nel corpus che vogliamo analizzare, infatti, T-Lab ha individuato 1.699 parole chiave e 597 contesti elementari: le matrici corrispondenti, quindi, sono un po’ più grandine… Ma veniamo al nostro problema specifico: abbiamo una raccolta di articoli provenienti da due quotidiani, selezionati per data e argomento, e vogliamo cercare di capire, utilizzando T- Lab, come i due giornali riportano fatti di cronaca afferenti allo stesso argomento e come danno conto delle reazioni conseguenti. Volendo confrontare tra loro due (o più) testi, la prima domanda da porsi è se esistano, e in caso quali siano, i lemmi che li caratterizzano. Nel software risponde a tale quesito la funzione specificità, che individua le parole “tipiche” e quelle “esclusive” di ogni testo. Le prime sono quelle che compaiono in entrambi i testi ma con frequenza significativamente maggiore in uno dei due. dove l’avverbio “significativamente” ha un significato ben preciso in termini di chi quadro, un indice statistico che serve per testare se le frequenze osservate coincidono o meno con quelle “attese”. Le seconde, invece, sono le parole che compaiono esclusivamente in uno dei testi, con maggiore o minore frequenza: nel nostro caso, per esempio, “formazione_ professionale” e “governo” sono specificità esclusive di uno dei due quotidiani analizzati (quale?), mentre l’altro ha come specificità esclusive “maturità” e “aziendale”. “Lavoratore” e “infortunio” sono invece parole tipiche del primo, mentre “studente”, “ragazzo” e anche “stage” lo sono del secondo.

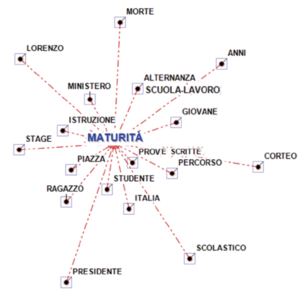
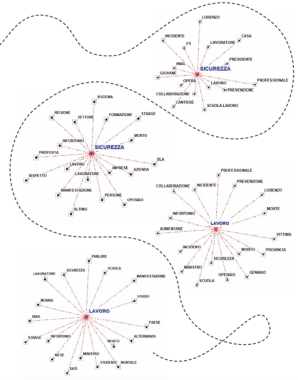
Tramite le analisi descritte fino a questo momento, riusciamo a farci un’idea di quali siano le parole chiave presenti in entrambi i documenti o tipiche/esclusive dell’uno o dell’altro. Lo strumento dell’associazione di parole consente adesso di capire meglio come si sviluppa il discorso nei due contesti. Per ogni parola che reputiamo significativa, infatti, il suo grafico delle associazioni permette di visualizzare tutte le parole che le sono più frequentemente associate all’interno del testo selezionato. Consideriamo per esempio la parola “maturità” che, come si diceva, è esclusiva degli articoli di uno dei due quotidiani. La funzione “associazioni di parole”, applicata a questi articoli, produce un grafico (vedi figura) in cui il lemma selezionato (“maturità”, appunto) è evidenziato in blu e gli altri lemmi, in nero, sono distribuiti attorno, a distanza inversamente proporzionale al grado di associazione di ognuno con la parola “maturità”. Facendo doppio click su ogni lemma nero che compare nel grafico, si apre una finestra che elenca tutti i paragrafi in cui quel lemma compare associato a quello blu (le cosiddette co-occorrenze): in altri termini, con un semplice click sui box relativi possiamo verificare se l’interpretazione “durante il corteo in memoria del giovane Lorenzo morto durante uno stage per l’alternanza scuola-lavoro gli studenti si sono lamentati per la reintroduzione delle prove scritte alla maturità” sia quella corretta o sia solo una interpretazione maligna. La distanza tra due lemmi neri, invece, non ha alcun significato: le relazioni significative, cioè, sono del tipo uno-a-uno, tra il lemma blu e ciascuno degli altri. In altri termini, il grafico non significa affatto che negli articoli del quotidiano in esame ci sia un accostamento insistente tra studente e piazza, né tra ministero e alternanza scuola-lavoro. Per poter costruire grafici di questo tipo, T-Lab deve stabilire, dato un qualunque lemma presente nel testo (chiamiamolo lemma B), a quale distanza collocarlo rispetto al lemma blu (lemma A). Tale distanza si calcola attraverso il cosiddetto coefficiente del coseno, la cui formula è la seguente:

dove con occ(X) indichiamo il vettore delle occorrenze del lemma X nei contesti elementari del testo in esame e i simboli ‹ , › e || || rappresentano rispettivamente il prodotto scalare e la norma euclidea. Il coefficiente del coseno è quindi un numero compreso tra 0 e 1, che è nullo se e solo se i termini non compaiono maiinsieme nel testo, ed è esattamente uno se e solo se le due parole compaiono sempre insieme. Fornisce, quindi, una misura della “vicinanza” tra il lemma B e il lemma A in tutto il testo in esame. La distanza tra il lemma A e il lemma B nel grafico è sostanzialmente il suo reciproco: sono infinitamente lontani da A (e dunque non compaiono nel grafico) i termini B con coefficiente del coseno 0, cioè quelli che non compaiono mai con A, e sono progressivamente più vicini quelli il cui coefficiente si avvicina a 1, cioè quelli che, quando compaiono, compaiono spesso insieme ad A. Se, ad esempio, presi in esame 10 contesti elementari, il lemma A compare nei primi cinque e nell’ultimo, mentre il lemma B compare nel primo, sesto e settimo, i due vettori delle occorrenze sono:

occ(A)= [1 1 1 1 1 0 0 0 0 1]

occ(B)= [1 0 0 0 0 1 1 0 0 0]

e il coefficiente del coseno è quindi:

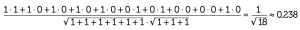
Otteniamo un valore basso che corrisponde al fatto che i due termini compaiono relativamente poco assieme (solo in 1 contesto su 10) mentre la prima parola appare spesso ma da sola (6 contesti su 10). Nel grafico quindi le due parole sono distanti. Vediamo nella pagina a fianco i grafici relativi a due delle parole più significative e più rappresentate negli articoli selezionati di entrambi i quotidiani, ovvero “lavoro” e “sicurezza”. Di fronte a grafici come questi la tentazione di fare inferenza è messaggio tutto sommato rassicurante: su un tema complesso come quello della sicurezza sul lavoro, evidentemente, c’è poco spazio per la polarizzazione politica e la richiesta di prevenzione non ha partito.