
Soluzioni del 17 giugno 2024 a cura di Fabio Ciuffoli
Ieri abbiamo presentato due giochi che hanno fatto parte delle gare internazionali di matematica negli ultimi anni e di seguito pubblichiamo le nostre proposte di soluzione.
Giardini, aiuole e prati – soluzioni
1. Una villa si affaccia sul lago con un grande giardino che deve essere piantumato e si decide di tenerlo in parte a prato e in parte coperto di fiori multicolore. Il giardino ha una forma che si può schematizzare con un trapezio isoscele ABCD le cui diagonali si incontrano in O come disegnato in figura. Si sa che le parti a prato misurano rispettivamente AOB, 50 m2 e DOC 32 m2. Quanto misurano le parti destinate ai fiori?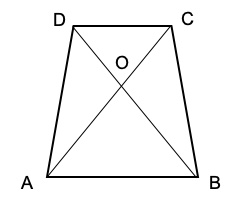 1. SOLUZIONE. Presentiamo due diversi modi per arrivare alla soluzione.
1. SOLUZIONE. Presentiamo due diversi modi per arrivare alla soluzione.
I. I due triangoli isosceli a prato DOC e AOB sono simili, con aree in rapporto 50/32 = 25/16. Le misure lineari sono quindi in rapporto √(25/16) = 5/4. Indicando con h1 l’altezza del triangolo AOB avremo h1 = 50 • 2 /AB = 100/AB. Allo stesso modo, indicando con h2 l’altezza del triangolo DOC avremo h2 = 64/DC. Abbiamo considerato che DC = (4/5)AB quindi sostituendo, avremo h2 = 64/ [(4/5) AB] che diviene h2 = 80/AB. L’area totale del trapezio è (AB + (4/5)AB ) • (100/AB + 80/AB)] /2 = [(9/5)AB • 180/AB] /2. Semplificando 9/5 • 180/2 = 162. Infine 162 – 50 – 32 = 80 m2 è l’area totale delle parti da coprire con fiori.
II. Indichiamo con X le aree dei due triangoli congruenti, con S1 e S2 le aree note rispettivamente di 50 m2 e 32 m2 come disegnato in figura.
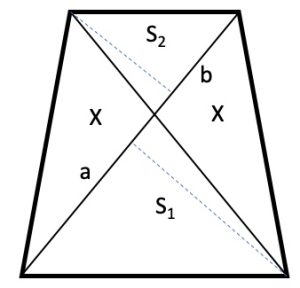
Sappiamo che due triangoli con uguale altezza hanno le aree proporzionali alle rispettive basi. In questo caso i quattro triangoli hanno basi comuni che abbiamo indicato con a e con b. Precisamente i triangoli X e S2 hanno uguale altezza perciò X = bh/2 e S2 = ah/2 per cui X/S2 = b/a. Lo stesso vale per i triangoli S1 e X per cui S1/X = b/a. Consegue che X/S2 = S1/X. Da cui X2 = S1 • S2 che diviene X = √(50 • 32) = 40 m2.
2. Il disegno seguente rappresenta, in pianta, un giardino. L’area verde del rettangolo è uguale all’area della cornice piastrellata bianca. Trovare i valori interi in metri delle dimensioni del rettangolo verde in modo che l’area sia la minima possibile.
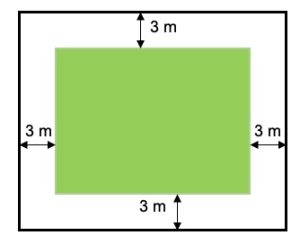 2. SOLUZIONE. Diverse e interessanti proposte di soluzione sono state indicate nei commenti. Noi presentiamo la soluzione empirica per tentativi e un breve cenno alla soluzione teorica che prevede l’utilizzo di un’equazione di secondo grado.
2. SOLUZIONE. Diverse e interessanti proposte di soluzione sono state indicate nei commenti. Noi presentiamo la soluzione empirica per tentativi e un breve cenno alla soluzione teorica che prevede l’utilizzo di un’equazione di secondo grado.
Indichiamo con a e con b i due lati del rettangolo verde.
ab = (b + 6) • (a + 6) – ab
2ab = ab + 6b + 6a + 36
ab = 6b + 6a + 36
ab – 6a = 6b + 36
a(b – 6) = 6b + 36
a = (6b + 36) / (b – 6) quindi b deve essere intero e maggiore di 6. I valori possibili di b e a sono:
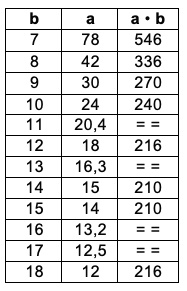
In modo empirico troviamo i valori di a e b, che danno l’area minima del rettangolo verde e della cornice, che sono 14 e 15 o viceversa (14 • 15 = 210 m2).
Per la dimostrazione teorica occorre impostare un’equazione di secondo grado con la derivata si individua il minimo e considerando i valori interi adiacenti si trova il risultato.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
3 risposte
Problema 1. L’altezza del trapezio sia h e x quella di ABO così l’altezza di DCO è h-x e siano AB = b DC = a. Ciò posto; x^2 : (h-x)^2 = 50 : 32 da cui x = 5.h/9 e pure b^2/a^2 = 50/32 per cui b = 5.a/4 e b.x = 100 ossia (5.a/4).(5.h/9) = 100 e a.h = 144. Ma si ha: a.h/2 – 32 = b.h/2 – 50 da cui b.h – a.h = 36 e b.h = 36 + 144 = 180. Pertanto Area fiori = S = (a.h+b.h)/2-82 = (144+180)/2-82 = 80 mq.
x e y = lati orizz e vert AreaVerde
AreaBianxa = 3*perimetro asse medio =
= 3*[2*(x+3)+2*(y+3].
AreaVerde=AreaBianca
xy=6x+6y+36 da cui y=(6x+36)/(x-6)
A=xy=(6x^2+36x)/(x-6)
Introducendo valori numerici interi di x si trova, numericamente, x=14 y=15 o viceversa e A=210.
Ottimo