
I Giochi del Lunedì di Prisma del 12 agosto 2024 a cura di Fabio Ciuffoli
Oggi proponiamo due giochi tra geometria e calcolo delle probabilità. Invitiamo i lettori a inviarci osservazioni e proposte di soluzione utilizzando lo spazio riservato ai commenti.
Probabilità, cerchi e circonferenze
1. Qual è la probabilità di colpire a caso, all’interno di un cerchio, un punto più vicino al centro anziché alla circonferenza esterna? (I colpi fuori dal cerchi non sono conteggiati)
2. Prendendo due punti casuali su una circonferenza quante probabilità si hanno di avere una distanza tra di loro minore del raggio r?
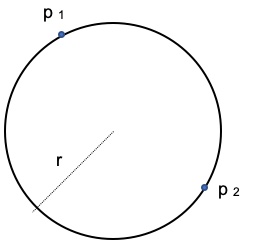
Aggiornamento per le soluzioni click qui.
L’immagine in evidenza è di Robert Delaunay – Rhythm No. 1.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
11 risposte
Riguardo al problema 1 si deve fare il rapporto tra l’area della circonferenza concentrica al bersaglio di raggio pari alla metà del raggio del bersagio e l’area del bersaglio stesso. Come è noto il rapporto tra aree di figure simili e pari al quadrato del rapporto tra segmenti corrispondenti, quindi la probabilità richiesta è 1/4.
Per il problema 2, Il primo punto P può stare ovunque. A partide da P disegnamo l’esagono regolare inscritto nella circonferenza e indichiamo con A e B i due vertici più vicini a P.
Come è noto, l’esagono regolare inscritto in una circonferenza ha i lati uguali al raggio della circonferenza, quindi il secondo punto Q si trova a distanza minore o uguale al raggio se si trova nell’arco AB che contiene P. Evidentemente tale arco è lungo un terzo della circonferenza, quindi la probabilità richiesta è 1/3.
Prova 1
https://math.stackexchange.com/questions/3397331/probability-of-euclidean-distance-between-two-random-points-inside-a-unit-circle?fbclid=IwY2xjawEoPqxleHRuA2FlbQIxMAABHQTuhwpwyVNzAIAYLvdkncScqdaNrSRwCpB7MnXsZQtkjsgt2BfR30dqtg_aem_sKE5ikNwMnucs-KKwKTNkA
2. Più interessante se i 2 punti sono presi a caso nel cerchio…
Riporto un interessante scambio di opinioni tra Antonio Fanari e Giorgio Vecchi su un social media di divulgazione matematica.
Antonio Fanari: Nel caso di distribuzione uniforme canonica
P(||P₁-P₂||≤r)=61/48-√3/π
P≈0.719504437…
Nel caso di distribuzione uniforme nel piano cambia la p.d.f. e si dimostra che:
P(||P₁-P₂||≤r)=1-3√3/(4π)
ossia
P(||P₁-P₂||≤r)≈0.586503328…
Giorgio Vecchi a Antonio Fanari: come arrivi a quel risultato? Io però trovo un valore diverso: ~0.58650.
Antonio Fanari a Giorgio Vecchi: ho fatto una ricerca sul web, il problema è tosto forse è sbagliata la soluzione che ho postato perché un altro link da la tua soluzione.
Ti invio i link:
la tua soluzione:
https://math.stackexchange.com/…/probability-that-the…
quella che ho postato io:
https://math.stackexchange.com/…/probability-of…
Probability that the distance between two random points inside a circle is less than some value
MATH.STACKEXCHANGE.COM
Probability that the distance between two random points inside a circle is less than some value
Probability that the distance between two random points inside a circle is less than some value
Antonio Fanari a Giorgio Vecchi: forse è corretta la tua anche perché è in accordo con la simulazione, il problema a quanto pare su cui discutono è la definizione di distribuzione uniforme entro un disco, per wolfram ad esempio la distribuzione uniforme è questa e porta a una specifica distanza media:
https://mathworld.wolfram.com/DiskLinePicking.html
Wolfram MathWorld: The Web’s Most Extensive Mathematics Resource
MATHWORLD.WOLFRAM.COM
Wolfram MathWorld: The Web’s Most Extensive Mathematics Resource
https://math.stackexchange.com/questions/2901090/probability-that-the-distance-between-two-random-points-inside-a-circle-is-less?rq=1&fbclid=IwY2xjawEoPhVleHRuA2FlbQIxMAABHT1jWBRPLFSsDjYSiBuNOvTXIB4ygDEzz1hO-xHIdTw-0Y1sDbeXU7vbIA_aem_GSN_KyDrYWEGb7mg-ehePQ
1. Si tratta di pesare l’area del cerchio di raggio r/2: pi(r/2)^2
rispetto a quella del cerchio che lo contiene di raggio r: pir^2
Quindi la probabilità è 1/4
2. La distanza di due punti sulla circonferenza è minore di r se i rispettivi raggi formano un angolo minore di 60° o maggiore di 300°
Quindi 120°/360°=1/3
Quesito n.1: 1/4.
Quesito n.2: 1/3.
Buongiorno Luigi, secondo me manca una considerazione per completare il ragionamento e quindi il risultato. A domani per un confronto e per la soluzione commentata.
Vero, hai ragione, non ho tenuto conto del fatto che P1 è uno spigolo comune a 2 lati dell’esagono. Quindi la probabilità cercata è 2/6
Problema 2. Enunciato lo scriverei così:
Dato un punto qualsiasi P1 su una circonferenza, quale è la probabilità che, scegliendo un altro punto a caso P2, la sua distanza da P1 sia minore della sua distanza dal centro della circonferenza.
Per risolverlo basta considerare che la distanza tra due punti della circonferenza equivale alla loro distanza dal centro quando essi sono i vertici di un lato di un esagono regolare… per cui la probabilità cercata è 1/6