
I Giochi del Lunedì di Prisma del 20 febbraio 2023 a cura di Fabio Ciuffoli
Oggi proponiamo tre giochi, prendendo spunto da una raccolta di enigmi matematici giapponesi del 1721. Invitiamo i lettori a inviarci le loro osservazioni e proposte di soluzione utilizzando lo spazio relativo ai commenti. Domani alle ore 17.00 pubblicheremo le soluzioni.
Wakoku: enigmi giapponesi
1. In ognuno dei quattro settori del cerchio esterno c’è un numero a due cifre, 10, 12, 20 e 18, che è uguale alla somma dei tre numeri agli angoli del suo settore. Ad esempio 10 = 3 + a + b oppure 12 = 3 + b + d e via di seguito. Collocare nei cerchi, a, b, c, d, i numeri da 1 a 9 sapendo che ogni numero va utilizzato solo una volta.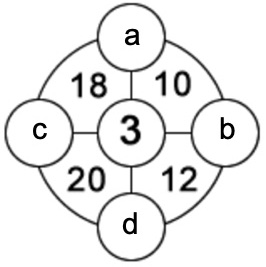
2. Scrivi i numeri da 1 a 9 nei cerchi neri in modo tale che la somma dei numeri attorno a ciascun cerchio blu, compreso il numero nel cerchio centrale, e lungo le linee orizzontali e verticali sia la stessa. Si tratta di quattro somme di cinque numeri ciascuna che devono dare lo stesso importo.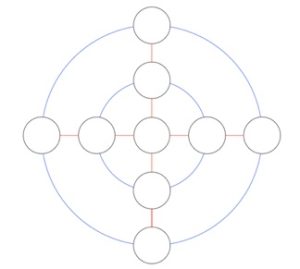
3. Infine presentiamo il gioco apparso in rete su un forum di Singapore e riprodotto nell’immagine seguente. La domanda chiede: “Studia lo schema numerico. Completa i numeri mancanti.” Nessuna gomma da masticare consentita!

La foto pare ritoccata e le istruzioni non sembrano adeguate. Il problema è stato prelevato e modificato da un sito web di enigmi matematici gestito da Gordon Burgin. Nel problema originario, quello da noi proposto al gioco n. 1, il quadrante in basso a sinistra ha un 20. Nella versione di Singapore lo 0 è cancellato e c’è il 2. Non c’è da stupirsi che non ci sia una soluzione ovvia! Ecco allora proponiamo un terzo problema:
Aggiornamento per le soluzioni click qui.
Il primo gioco è tratto dal sito web di enigmi matematici gestito da Gordon Burgin un insegnante americano in pensione a Norwich. Il secondo gioco è tratto dalla raccolta di enigmi giapponesi del 1721 Wakoku Chie-Kurabe di Kan Chu Sen. Il terzo gioco è una rielaborazione apparsa su un forum matematico di Singapore.
L’immagine in evidenza è tratta dalla raccolta Wakoku Chie-Kurabe di Kan Chu Sen.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
14 risposte
Problema 2. Vedere allegato.
1+2+…..+9=45, 45/9=5, viene al centro. Poi ogni cerchio e ogni diametro escluso il centro fa una somma di 40/2, cioè 20.
Ma ci sono certamente diverse soluzioni.
Problema 1
A=6 B = 1 C = 9 D= 8
Problema 3
Ho pensato a una situazione problematica
adatta a una classe 5 della scuola primaria : inserite nei cerchi vuoti i numeri 5 9 15 e 45.
Perché questi numeri ?
Soluzione : sono tutti divisori della somma dei numeri già scritti,cioè 45.
Bene, ottima idea per la soluzione al problema 3. Nel pomeriggio le nostre proposte di soluzione.
Si risolve facilmente con un sistema lineare quadrato di ordine 4: si vede facilmente che il determinante associato è non nullo, quindi la soluzione è unica. 3+a+c=18, 3+a+b= 10, 3+ b+d= 12, 3+d+c= 20. Questo è ovviamente equivalente al sistema a+c= 15, a+b=7, b+d=9, d+c=17. La soluzione si trova facilmente per sostituzione, a= 6, b= 1, c=9, d=8.
Problema 1. Facile. 4 incognite e 4 equazioni. Con un sistemino si risolve tutto
Si risolve facilmente con un sistema lineare quadrato di ordine 4: si vede facilmente che il determinante associato è non nullo, quindi la soluzione è unica. 3+a+c=18, 3+a+b= 10, 3+ b+d= 12, 3+d+c= 20. Questo è ovviamente equivalente al sistema a+c= 15, a+b=7, b+d=9, d+c=17. La soluzione si trova facilmente per sostituzione, a= 6, b= 1, c=9, d=8.
Problema n° 2: vedi allegato.
Enigma 2.
In verticale: 96152
In orizzontale: 34178
Al centro: 1
Problema 2.
Vista la simmetria, mipare che la soluzione possa essere la più semplice ipotizzabile.
In verticale: 1, 3, 5, 7, 9; in orrizzontale: 6, 2, 5, 8, 4.
Al centro c’è il 5 ed ogni somma è 25.
Ottimo. Domani pomeriggio tutte le soluzioni.
1 – La spiegazione confonde: non bisogna “collocare i numeri da 1 a 9”, ma “quattro numeri compresi tra 1 e 9”.
La soluzione è banale: visto che c+d = 17 i due numeri possono essere solo 8 e 9, e d deve essere 8, perché sommato a 3+b fa 12. quindi b=1 ed a= 6.
Ottimo chiarimento sul testo.
Problema 1. A = 6, B = 1, D = 8, C = 9.
Enigma 1.
6-1-8-9