
I Giochi del Lunedì di Prisma del 13 febbraio 2023 a cura di Fabio Ciuffoli
Oggi presentiamo tre problemi di geometria proposti del sito web di matematica ricreativa Dare2Solve. Il sito è interessante sia per i contenuti che per l’ottima grafica. Invitiamo i lettori a inviarci le loro osservazioni e proposte di soluzione utilizzando lo spazio riservato ai comenti. Domani alle ore 17.00 pubblicheremo le soluzioni.
Osare la soluzione!
1. Dal vertice in basso a sinistra del quadrato, vengono tracciati due segmenti inclinati dello steso angolo α, che intersecano due lati del quadrato nei punti indicati a distanza rispettivamente di 4 e 6. Calcolare l’area blu compresa tra i due segmenti e i lati del quadrato.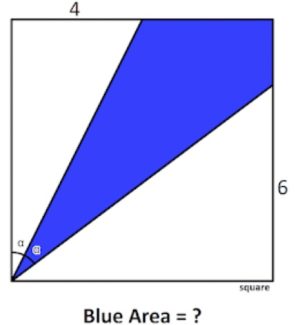
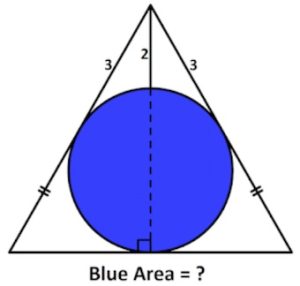
2. Calcolare l’area blu.
3. Calcolare l’area blu.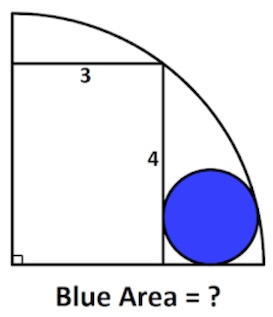
Aggiornamento per le soluzioni click qui.
I problemi sono tratti, con opportune rielaborazioni, dal sito web Dare2Solve https://dare2solve.com
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
16 risposte
Problema 1 area blu 24
Problema 3 Il diametro del cerchio blu è quasi 2 per cui l’area è quasi 3,14
Bene la 1. Nel pomeriggio tutte le soluzioni.
1. Il cateto lungo 4 è opposto all’angolo α, l’angolo compreso tra il cateto lungo 6 e il secondo segmento è 2α. Pertanto il lato del quadrato e cateto opposto a 2α, vale 8. Pertanto l’area del quadrato è 64, l’area del triangolo rettangolo con cateti 4 e 8 è 16, l’altro con cateti 6 e 8 è 24. L’area blu è 64-(16+24)=24
3. Il raggio del quarto di cerchio è pari alla diagonale del rettangolo 3X4 cioè 5. Il diametro del cerchio blu è 5 – 3= 2 quindi l’area è pigreco
Bene la risposta 1. Da rivedere la 3. A domani per le soluzioni
Problema n° 1. Soluzione meno semplice ma elegante. vedi immagine
Problema 2. 3^2+r^2= (r+2)^2 -4r=-5 r=5/4= 1,25 A cerchio blu 3,14×1,25^2= 4,9
Problema 1. vedi immagine
Problema 1. L = 4/(tg α) = 6 / (tg (90°-2α) )
4 ctg 2α = 6 tg α
4 ( (1-tg2 α)/(2 tg α) ) = 6 tg α
2 = 8 tg2 α
tg α = 1/2
L = 8
Area blu = 64 – 24 – 16 = 24
Massimo Molinelli
Problema n° 1: →Area Blue = 24.
Problema n° 2: →Area Blue = 25/16•π.
Problema n° 3: → Vedi contributo visivo
1) 24, utilizzando la trigonometria, 12cos^3(a)+8cos^2(a)-12cos(a)-4, cos(a)=\/3/2, a=30°, lato quadrato=8, Area=l^2-5l=24;
2) Pitagora, 9+r^2=(r+2)^2, r=5/4, Area=pi 25/16;
3) risolto in gruppo mat. Pi(144-16\/80)
a=26,56°, non 30° per cui confermo il resto lato=8…
Problema 3.
1. Aree triangoli bianchi 16 e 24, area quadrato 64, area blu 24
Problema 2.
Con Pitagora applicato al triangolo di lati R, 3 e 2+R (ipotenusa) trovo R=1,25.
Per cui area del cerchio blu A=4,91
1. 24
2. 25/16 * PI
3. 16(rad(5)-2)^2 * PI
Perfetto. A domani per le soluzioni con dimostrazione.