
I Giochi del Lunedì di Prisma del 22 agosto 2022 a cura di Fabio Ciuffoli
Oggi proponiamo quattro giochi matematici e logici che privilegiano l’aspetto intuitivo e si possono risolvere senza effettuare calcoli elaborati. Invitiamo i lettori a inviarci osservazioni e proposte di soluzione, utilizzando lo spazio riservato ai commenti. Domani alle ore 17.00 pubblicheremo le soluzioni.
Senza calcoli
1. Il proprietario di un terreno, a forma di quadrato di lato 20 metri, ha deciso di affittare la parte in eccedenza accanto alle tre torri, delineato in rosso nella pianta in figura. Il terreno da affittare doveva essere destinato a una quarta torre, ora non più necessaria, più il terreno compreso tra le tre torri esistenti. Determinare l’area del terreno da affittare.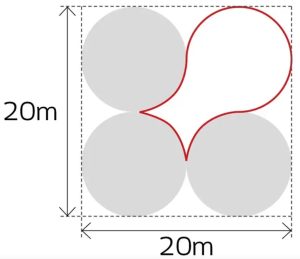
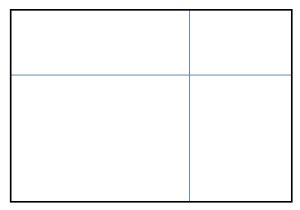
2. Un foglio di carta è stato diviso in quattro rettangoli come mostrato in figura. È evidente che il rettangolo in basso a sinistra ha l’area più grande e il rettangolo in alto a destra ha l’area più piccola. Senza effettuare misurazioni, come si può determinare se gli altri due rettangoli hanno la stessa area? E se no, quale dei due ha l’area maggiore?
3. Determinare l’area delle parti colorate in rosso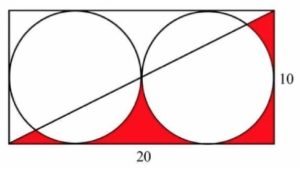
4. Quante libbre pesa l’ultimo piatto?
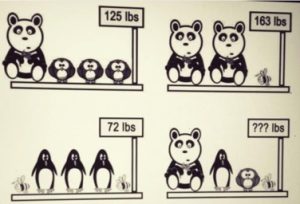
Aggiornamento per le soluzioni click qui.
Il problema 1 è tratto sito web New Scientist. Il problema 2 è tratto da Arithmetical, Geometrical and Combinatorial Puzzles from Japan di Tadao Kitazawa. Il problema 3 è facilmente reperibile in rete, infine il problema 4 è un vecchio gioco con l’immagine originale inglese.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
15 risposte
Primo:
Area quadrato 400
Area ciascun cerchio 25pi
Si dividono l’area differenza 16 quasi triangoli uguali. Ciascuno dei quali di area 1/4*(100-25pi).
Dunque … area contornata rosso =100 i
Perfetto
Per il problema 2., specifico anche che, nel disegno proposto, l’incrocio NON cade sulla diagonale, ergo il rettangolo in basso a destra ha area maggiore di quello in alto a sinistra. vedi figura allegata
per il problema 2 provo a proporre questa soluzione:
se il vertice comune ai 4 rettangoli è nella parte di rettangolo “grande” al di sopra della diagonale tracciata dal vertice in basso a sinistra al vertice in alto a destra del rettangolo “grande”, il rettangolo in alto a sinistra è più piccolo del rettangolo in basso a destra ;
viceversa se il vertice comune ai 4 si trova al di sotto della diagonale .
Se il vertice comune ai 4 è sulla diagonale, i 2 rettangoli sono uguali.
Perfetto, un disegno aiuterebbe la comprensione della spiegazione. Nel pomeriggio la soluzione argomentata.
A 100mq
C 21,5 mq
D 120 libbre
Bene A e D. A domani per le soluzioni.
Problema 4. 80 il panda, 15 il Calimero???, 22 il pinguino, 3 la vespa
Pieghi il foglio lungo la diagonale e se l’incrocio è sulla piega le due aree sono sicuramente uguali.
Se l’incrocio cade fuori non possiamo dire nulla, ma il problema non chiede il caso generale ma “quel” caso dove il foglio “è stato diviso”.
1. 100mq
2. Traslando il rettangolo più piccolo sui rettangoli da confrontare e così via
3.21,5mq
4.120ibs
Perfetto, a domani per le soluzioni con argomentazione.
1) L’aggiunta rispetto al cerchio è pari alle tre parti mancanti per formare il “quarto di quadrato” della torre assente. Quindi area pari a 100 metri quadrati.
2) Se i due segmenti divisori passassero per il centro del rettangolo grande tutti i rettangolini sarebbero congruenti. Spostando quello orizzontale verso l’alto come in figura faccio diminuire l’area del rettangolo in alto a sinistra e aumentare quella di quello in basso a destra di una frazione pari allo spostamento diviso per la lunghezza originale del mezzo lato. Spostando quello verticale verso destra come in figura succede una cosa analoga di segno opposto. chiamando A e B i lati del rettangolo grande si può capire quale dei rettangoli in questione è più esteso confrontando gli spostamenti dal centro DeltaA e DeltaB rispetto alle lunghezze totali A e B. Se DeltaA/A > DeltaB/B è più grande un rettangolino altrimenti è più grande l’altro. Sono equiestesi se vale l’uguaglianza.
3) Le parti in rosso stanno in mezzo rettangolo a cui vanno tolte due parti cerchio che hanno somma pari al cerchio intero. Quindi l’area rossa è pari a 20X10/2-PigrecoX25=100-25Pigreco.
4) Sommando i primi tre piatti otteniamo 3 volte il quarto piatto. (125+163+72)/3=120.
Perfetto. Un disegno aiuterebbe la comprensione della risposta 2. A domani pomeriggio per le soluzioni.
Problema n 4. Bellissimo.. somma tutto e dividi per 3..120
100 mq… però 10×10 è un calcolo😁