47. Soluzioni del 6 giugno 2022 – Il gioco del serpente e la tavoletta di cioccolato

Le soluzioni del 6 giugno 2022 a cura di fabio Ciuffoli

Ieri abbiamo presentato due giochi di strategia e ora pubblichiamo le soluzioni con le dimostrazioni  

Il gioco del serpente e la tavoletta di cioccolato

1. Il gioco del serpente.  Si svolge su una scacchiera, di n righe e n colonne, tra due giocatori. Alberto inizia segnando un quadrato a sua scelta, Benedetta a sua volta segna un quadrato adiacente ortogonalmente. Successivamente, Alberto e Benedetta continuano ad alternarsi, ciascuno segna un quadrato ortogonale all’ultimo contrassegnato, creando così un serpente sulla scacchiera. Perde il giocatore che non è in grado di segnare un ulteriore quadrato. Quali quadrati di partenza, se ce ne sono, portano Alberto a vincere?

1. SOLUZIONE. Se proviamo il gioco con n relativamente piccolo, scopriremo che Benedetta vince sempre quando n è pari e che Alberto può vincere quando n è dispari. 

Per n pari, la scacchiera (n x n) viene facilmente ricoperta da rettangoli, tipo domino, che coprono due quadrati ortogonalmente adiacenti. Questo permette a Benedetta una facile strategia vincente, segnando l’altra metà di qualsiasi rettangolo tipo domino iniziato da Alberto e perciò Alberto non ha alcuna prima mossa vincente. Ad esempio in una scacchiera 2 x 2, dove abbiamo disegnato con colori diversi le celle ortogonali, qualsiasi scelta iniziale di Alberto permette la vincita di Benedetta.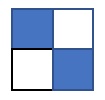 

La situazione cambia per n dispari. Dal momento che c’è un numero dispari di celle, non è possibile coprire la griglia con i rettangoli tipo domino e quindi una cella verrà sempre tralasciata. Se Alberto inizia scegliendo una cella maggioritaria, avrà quindi una strategia vincente. Generalizzando, se n è dispari Alberto avrà una strategia vincente purché inizi da una cella di colore maggioritario, come quelle grigie in figura, quindi o una cella d’angolo o la centrale.

2. La tavoletta di cioccolato.  Nella tavoletta di cioccolato, schematizzata in figura, il quadratino in alto a sinistra nasconde un pezzetto di aglio. Un primo giocatore taglia la tavoletta in due parti lungo una qualsiasi linea, verticale o orizzontale, di divisione dei quadretti e tiene per sé una parte e consegna al secondo giocatore l’altra parte. Il secondo giocatore deve proseguire la suddivisione con le stesse modalità. Perde chi è costretto a prendere il quadratino con l’aglio. Esiste una strategia vincente per il primo o il secondo giocatore?

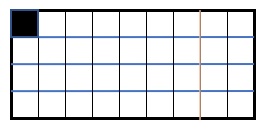
2. SOLUZIONE. Esiste una strategia vincente per il primo giocatore: dovrà lasciare all’avversario una porzione di forma quadrata.  Chi riceve un pezzo di cioccolato di forma rettangolare, con il lato minore uguale a un solo quadretto, ha la possibilità di vincere immediatamente, isolando con un’unica mossa il quadretto all’aglio e lasciandolo così all’avversario come illustrato in figura seguente.

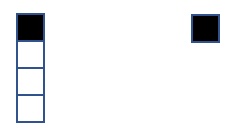
Ora in generale, suddividendo un quadrato si possono ottenere solo rettangoli, mentre se si divide un rettangolo e sempre possibile ottenere un quadrato. Di conseguenza, il primo giocatore ha l’opportunità di ottenere un fondamentale vantaggio consegnando all’avversario sempre una porzione di forma quadrata, come in figura seguente.

La strategia vincente consiste nel lasciare all’avversario, a ogni mossa, una porzione di forma quadrata in modo che questo ne possa generare solo una di forma rettangolare.

A lunedì prossimo.