
Le soluzioni del 28 marzo 2022 a cura di Fabio Ciuffoli
Ieri mattina abbiamo proposto cinque giochi prendendo spunto dallo storico Problema dei Sette Ponti di Königsberg e dalla Teoria dei Grafi di Eulero. Presentiamo di seguito le soluzioni con dimostrazione.
Kaliningrad e le passeggiate di Eulero – soluzioni
1. I sette ponti. Il fiume Pregel, che attraversa la città di Königsberg, crea due isole unite alla terraferma per mezzo di sei ponti, mentre un ponte unisce tra loro le due isole, come illustrato in figura. Il problema, che ha stimolato la curiosità degli abitanti durante le passeggiate domenicali, riguarda proprio i suoi sette ponti.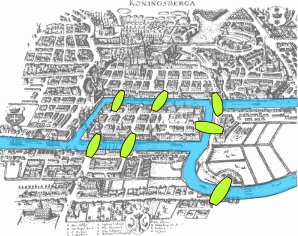 È possibile trovare un percorso a piedi per la città in modo da attraversare una e una sola volta tutti e sette i ponti?
È possibile trovare un percorso a piedi per la città in modo da attraversare una e una sola volta tutti e sette i ponti?
1. SOLUZIONE. Il problema si può ricondurre alla seguente figura. Il grafo a destra è costituito da quattro nodi A, B, C e D. I nodi C e B che rappresentano le due sponde di terraferma e i nodi A e D rappresentano le due isolette e sono collegati tra loro attraverso sette archi, che rappresentano i ponti. A questo punto sono possibili due strategie di soluzione. La prima, empirica, cercando tute le possibili combinazioni di percorso e verificare se ci sono soluzioni, procedura lunga e complessa e poco utile in casi dissimili. La seconda, teorica, proposta da Eulero con il noto Teorema: “Definendo il grado di un nodo come il numero di archi che si connettono a tale vertice, è possibile passare dal nodo X al nodo Y, diverso da X, attraversando una e una sola volta tutti gli archi se e solo se gli unici nodi di grado dispari sono proprio X e Y. Se X coincide con Y, è possibile passare una e una sola volta tutti gli archi se e solo se tutti i nodi sono di grado pari. Un grafo che contiene più di due nodi dispari non è percorribile senza sovrapposizioni di percorso”.
Il grafo a destra è costituito da quattro nodi A, B, C e D. I nodi C e B che rappresentano le due sponde di terraferma e i nodi A e D rappresentano le due isolette e sono collegati tra loro attraverso sette archi, che rappresentano i ponti. A questo punto sono possibili due strategie di soluzione. La prima, empirica, cercando tute le possibili combinazioni di percorso e verificare se ci sono soluzioni, procedura lunga e complessa e poco utile in casi dissimili. La seconda, teorica, proposta da Eulero con il noto Teorema: “Definendo il grado di un nodo come il numero di archi che si connettono a tale vertice, è possibile passare dal nodo X al nodo Y, diverso da X, attraversando una e una sola volta tutti gli archi se e solo se gli unici nodi di grado dispari sono proprio X e Y. Se X coincide con Y, è possibile passare una e una sola volta tutti gli archi se e solo se tutti i nodi sono di grado pari. Un grafo che contiene più di due nodi dispari non è percorribile senza sovrapposizioni di percorso”.
Nel caso dei ponti di Königsberg il nodo A è collegato con cinque archi/ponti, quindi è dispari di grado 5, mentre i nodi B, C, e D sono dispari di grado 3. La soluzione del problema dei ponti di Königsberg è allora a portata di mano: ogni nodo del grafo è di grado dispari, quindi la risposta è no, non esiste un tale percorso. Con buona pace dei passeggiatori della domenica, che camminano a braccetto del Lungo Pregel, sperando di riuscire un giorno a compiere l’impresa per poi vantarsene con gli amici al successivo tè in salotto.
2. La busta da lettera. Sapreste disegnare il grafo qui sotto, senza mai staccare la penna dal foglio e percorrendo ogni segmento una sola volta? 2. SOLUZIONE. Riassumiamo il teorema precedente. Tracciare un disegno con un solo tratto di penna, senza ripassare su una linea già tracciata, è possibile quando:
2. SOLUZIONE. Riassumiamo il teorema precedente. Tracciare un disegno con un solo tratto di penna, senza ripassare su una linea già tracciata, è possibile quando:
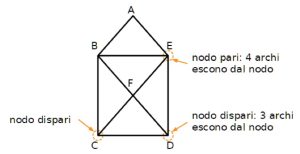
In questo caso della busta da lettera la risposta è affermativa, infatti si può disegnare il grafo partendo dal punto C oppure dal punto D. Ci sono diverse soluzioni possibili, qui ne riportiamo due. Un’ulteriore precisazione, in questo problema è permesso incrociare le linee, ma presentiamo anche la soluzione in rosso nel caso in cui non fosse permesso l’incrocio delle linee.
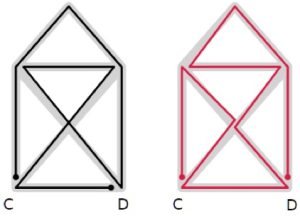 Abbiamo sdoppiato alcuni punti per facilitare la lettura. I punti di partenza/arrivo sono segnati con un bollino.
Abbiamo sdoppiato alcuni punti per facilitare la lettura. I punti di partenza/arrivo sono segnati con un bollino.
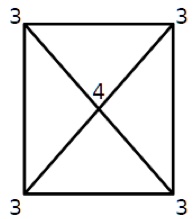
3. Il rettangolo con le diagonali. È possibile disegnare un rettangolo e le sue diagonali con un solo tratto di penna percorrendo tutti i segmenti ciascuno una sola volta? È possibile passare più volte sugli incroci.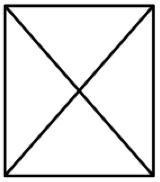
3. SOLUZIONE. Il rettangolo con le diagonali ha 4 nodi dispari, perciò non si può tracciare con un unico tratto di penna senza ripassare su una linea già tracciata.
4. Variazioni sui grafi. È possibile disegnare le seguenti figure senza mai staccare la penna dal foglio e senza ripassare su una linea già tracciata. È possibile passare più volte sugli incroci.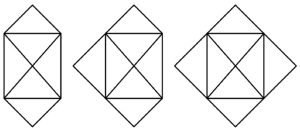
4. SOLUZIONE. La prima figura ha tutti i nodi pari, ciascuno dei quali può essere il punto di partenza di un circuito Euleriano. La seconda ha due nodi dispari, perciò si possono trovare diversi cammini Euleriani. La terza figura ha 4 nodi dispari, quindi non ha soluzioni.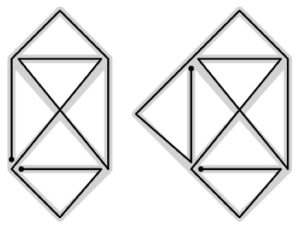
5. Tre dimensioni: colorare gli spigoli di un ottaedro. È possibile colorare tutti gli spigoli di un ottaedro con un pennarello rosso senza mai staccare la punta e senza ripassare su uno spigolo già colorato? Quale percorso deve seguire la punta del pennarello? È possibile passare più volte sui vertici.
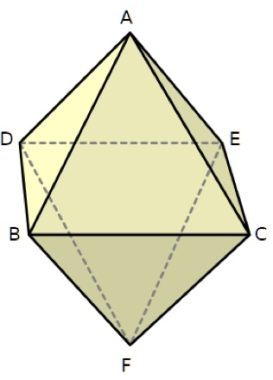 5. SOLUZIONE. Si può immaginare l’ottaedro come un grafo nello spazio: i vertici sono i nodi, gli spigoli sono gli archi. Ecco quindi una possibile soluzione.
5. SOLUZIONE. Si può immaginare l’ottaedro come un grafo nello spazio: i vertici sono i nodi, gli spigoli sono gli archi. Ecco quindi una possibile soluzione.
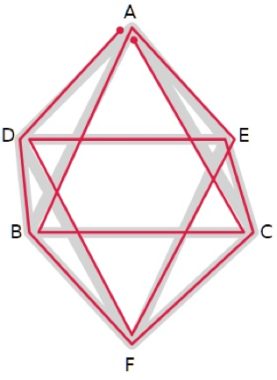 É interessante riportare la rete di collegamenti sul piano con un grafo equivalente.
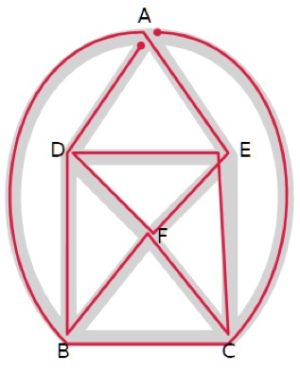
É interessante riportare la rete di collegamenti sul piano con un grafo equivalente.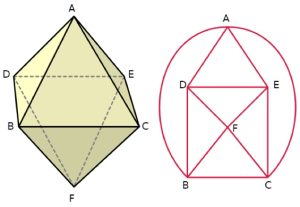 Ciascun nodo ha ordine pari, perciò esiste un circuito che passa per tutti gli archi. Nell’ordine il percorso passa per questi vertici: A, C, B, A, E, F, D, E, C, F, B, D, A.
Ciascun nodo ha ordine pari, perciò esiste un circuito che passa per tutti gli archi. Nell’ordine il percorso passa per questi vertici: A, C, B, A, E, F, D, E, C, F, B, D, A.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
Una risposta
Vorrei condividere un messaggio ricevuto da H. Sefa Akseki, un collega turco di Smirne, che ho avuto il piacere di conoscere in un corso di aggiornamento a Malta. Sefa mi ha scritto: “Ho risposto a malapena alla seconda domanda 🙂 ma ho chiesto ai miei studenti di 14 anni questa mattina a lezione… Hanno trovato facilmente la risposta e alcuni di loro mi hanno spiegato la logica dietro la domanda… Differenza generazionale… Grazie per aver condiviso e avermi dato la possibilità di iniziare la lezione con un’attività di socializzazione.”
Grazie Sefa.