I giochi del Lunedì di Prisma del 28 marzo 2022 a cura di Fabio Ciuffoli
Kaliningrad è oggi una exclave Russa, situata in posizione strategica sul Mar Baltico, tra Polonia e Lituania. Königsberg, questo era il nome dell’antica città della Prussia Orientale, è legata alla storia della matematica per il “Problema dei Sette Ponti” che, nel Settecento, ispirò Eulero per una prima formulazione della Teoria dei Grafi. Oggi proponiamo cinque giochi sulla Teoria dei Grafi. Invitiamo i lettori a presentarci osservazioni e proposte di soluzione nello spazio riservato ai commenti. Domani alle ore 17.00 pubblicheremo le soluzioni con dimostrazione.
Kaliningrad e le passeggiate di Eulero
1. I sette ponti. Il fiume Pregel, che attraversa la città di Königsberg, crea due isole unite alla terraferma per mezzo di sei ponti, mentre un ponte unisce tra loro le due isole, come illustrato in figura. Il problema, che ha stimolato la curiosità degli abitanti durante le passeggiate domenicali, riguarda proprio i suoi sette ponti.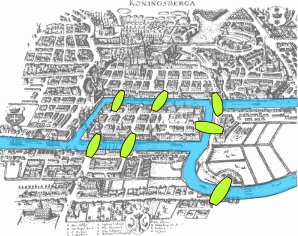
2. La busta da lettera. Sapreste disegnare il grafo qui sotto, senza mai staccare la penna dal foglio e percorrendo ogni segmento una sola volta?
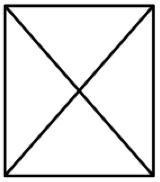
3. Il rettangolo con le diagonali. È possibile disegnare un rettangolo e le sue diagonali con un solo tratto di penna percorrendo tutti i segmenti ciascuno una sola volta? (È possibile passare più volte sugli incroci.)
4. Variazioni sui grafi. È possibile disegnare le seguenti figure senza mai staccare la penna dal foglio e senza ripassare su una linea già tracciata? (È possibile passare più volte sugli incroci.)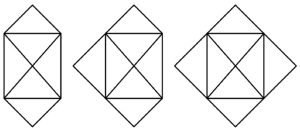
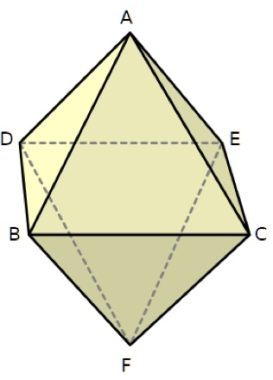
5. Tre dimensioni: colorare gli spigoli di un ottaedro. È possibile colorare tutti gli spigoli di un ottaedro con un pennarello rosso senza mai staccare la punta e senza ripassare su uno spigolo già colorato? Quale percorso deve seguire la punta del pennarello? (È possibile passare più volte sui vertici.)
Aggiornamento per le soluiozni click qui
I cinque problemi sono diffusamente presenti sul web. Abbiamo tratto la grafica e parte del testo dall’ottimo sito Base Cinque Appunti di Matematica Ricreativa.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
7 risposte
Ottaedro, vedi allegato.
Perfetto. Ottime integrazioni. Oggi pomeriggio le soluzioni con dimostrazione.
1) NO (vedi risposta precedente)
2) Casetta, sì (del resto ci abbiamo giocato tutti…) anche (ovviamente) per la regola del pari/dispari. Vedi allegato.
3) Barchetta, sì: mi riconduco alla casetta e aggiungo due segmenti. Spiegato anche con la regola del pari/dispari (vedi allegato).
4) Coso: sì, anche qui riconducendomi al caso precedente, e ovviamente anche per la regola solita (vedi allegato).
5) Quadrato: no (idem). Vedi allegato.
6) Ottaedro sì, vedi messaggio successivo.
1) No perchè ci sono 2 isole (nodi) con numero dispari di ponti (segmenti).
Se transito su un punto (isola o terraferma) i ponti che da quel punto partono devono essere in numero pari (tanti per entrare quanti per uscire, oppure tanti per andare quanti per tornare).
Anche se parto da un punto e lì torno avrò un numero pari di ponti ad esso connessi: numero pari per i passaggi più uno per la partenza e uno per il rientro a fine passeggiata.
Se parto da un punto e arrivo ad un altro punto, SOLO QUESTI DUE PUNTI devono avere un numero dispari di ponti (una partenza in più per il primo, un arrivo in più per l’ultimo).
Nell’immagine che allego, dove modellizza la situazione in 2 nodi (terraferma), 2 nodi (isole) i ponti (segmenti di collegamento dei nodi) sono sempre dispari, pertanto non potendo avere 4 tra punti di partenza e punti di arrivo il percorso non è tracciabile.
Per i quesiti successivi metto solo gli allegati; il testo è risultato un po’ ridondante.
Immagine da internet.
Bene a domani pomeriggio per le soluzioni
Io dico 1 no. Al 2 si partendo dal basso. 3 no. 4 due sì e uno no. 5 non so