Menu
Le soluzioni del 16 maggio 2022 a cura di Fabio Ciuffoli
Ragionare con i diagrammi di Venn – soluzioni
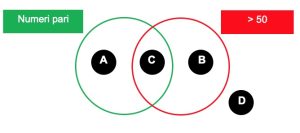
1. Per ciascuna delle regioni contrassegnate da A a D, scrivete alcuni numeri interi positivi che potrebbero appartenere a essa. Ogni cerchio rappresenta l’insieme dei numeri descritti dalla sua regola, il cerchio verde per l’insieme dei numeri pari e il cerchio rosso per l’insieme dei numeri maggiori di 50.
1. SOLUZIONE. La domanda chiedeva alcuni esempi. Ecco una possibile soluzione, ma ce ne sono tante altre.
2. Per ciascuna delle regioni contrassegnate da A a D, scrivete una frazione che potrebbe appartenere ad essa o eventualmente scrivete che è impossibile. Ogni cerchio rappresenta l’insieme delle frazioni descritte dalla sua regola, il cerchio verde per l’insieme delle frazioni maggiori di 1/5 e il cerchio rosso per l’insieme delle frazioni minori di ¼.
2. SOLUZIONE. La domanda chiedeva solo un singolo esempio. Ecco una possibile soluzione, ma ce ne sono infinitamente di più.
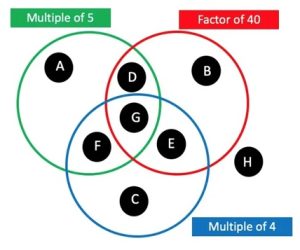
3. Per ciascuna delle regioni contrassegnate da A ad H sotto, scrivete un numero che potrebbe appartenere ad essa oppure scrivete che è impossibile. (Un fattore di un numero è un numero che si divide in quel numero senza resto).
3. SOLUZIONE. Ancora una volta, ecco solo una possibile soluzione.
4. Per ciascuna delle regioni contrassegnate dalla A alla H di seguito, scrivete cinque numeri che potrebbero appartenere ad essa oppure scrivete che è impossibile. La media [mean] è la somma dei numeri divisa per 5, la mediana [median] è il numero medio quando i numeri sono disposti in ordine crescente, la moda [mode] è il numero più comune e l'intervallo [range] è la differenza tra il numero più alto e quello più basso.
4. SOLUZIONE. Ecco una soluzione. Assumiamo che se tutti i numeri fossero diversi, allora tutti i numeri sarebbero la moda.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
5 risposte
Nel gioco 4 io avevo inteso 5 numeri nell’insieme verde, 5 nel blu, 5 nel rosso. Anche perché, trascurando il fatto che si ripetono gli stessi elementi in un insieme, la media o la moda o il range in tal caso andrebbe calcolato tra i 20 elementi dell’insieme o semplicemente non ho compreso il testo?
Ho lasciato il testo come proposto dal sito di Mr Barton Maths, traducendolo solo dall‘inglese. Ovviamente con qualche chiarimento in più, il solutore sarebbe stato agevolato (vedi anche il commento di Giuseppe). Comunque è stata un’ottima prova. A lunedì prossimo.
Assumendo, come ho fatto io, che se nessun numero si ripete non c’è la “moda”, allora F e G sarebbero impossibili 🙂
Sì è vero. Forse, per essere precisi, la condizione “se tutti i numeri fossero diversi, allora tutti i numeri sarebbero la moda” andava esplicitata nel testo del problema. Grazie per il contributo.
Per segnalare il seguente interessante confronto tra due lettori in relazione alla immagine in evidenza:
Silvio Capobianco: “Ah, il diagramma di Venn per quattro casi. Con i cerchi non si può fare.
Aggiornamento: non si può fare perché due circonferenze distinte si intersecano al più in due punti distinti, quindi il quarto cerchio aggiungerebbe al più 2×3 = 6 nuove regioni, invece delle otto necessarie”.
Patrizio Beraldo propone l’immagine seguente.
Silvio Capobianco: “Patrizio Beraldo Sono solo tredici regioni; ne mancano due”.
Patrizio Beraldo: “Silvio Capobianco vero non si può fare con le stesse caratteristiche.
Mancano le sovrapposizioni dell’area dei cerchi opposti. Un’opzione comunque interessante”.
Grazie per la partecipazione.