63. Soluzioni del 3 ottobre 2022 – Ragnatele, scudi e aree colorate

Le soluzioni del 3 ottobre 2022 a cura di Fabio Ciuffoli

Ieri mattina abbiamo presentato cinque giochi di natura geometrica e grafica. Alcuni richiedono qualche calcolo, mentre altri si risolvono con l’insight. Pubblichiamo ora le soluzioni argomentate. 

Ragnatele, scudi e aree colorate – soluzioni 

1. Esagono Ragnatela. Qual è il rapporto tra l’area gialla e l’area celeste? E qual è la somma delle lunghezze di tutti i tratti disegnati in nero?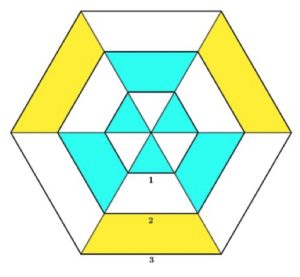1. SOLUZIONE.  Le varie aree si possono scomporre in piccoli triangoli equilateri uguali. Le aree celesti sono composte da 12 triangoli e le aree gialle da 15. Il rapporto è 15/12 o 5/4.  Per calcolare la lunghezza dei tratti disegnato in nero si possono seguire diversi metodi, noi proponiamo il seguente: 6 * 6 + 6 * 3 = 54. 

2. Trapezio colorato. Due cateti di un triangolo rettangolo isoscele misurano 50 cm ciascuno e sono stati divisi in 5 parti uguali. Determinare l’area della parte colorata.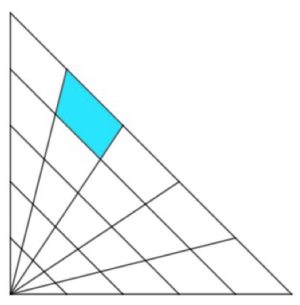

2. SOLUZIONE. Si calcola l’area del triangolo rettangolo di cateti 50 cm dalla quale si sottrae l’area del triangolo rettangolo di cateti 40 cm e poi si divide per 5. (50*50) /2 = 1.250 cm².  (40*40)/2 =  800 cm². (1.250 – 800)/ 5 = 90 cm². L’area della parte colorata è 90 cm^2.

3. Quattro triangoli. Trovare l’area di uno dei quattro triangoli rettangoli uguali.

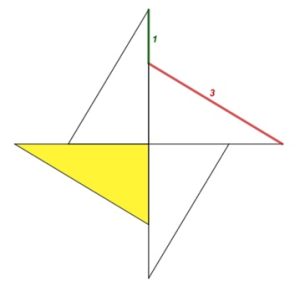
3. SOLUZIONE. Semplice e senza lunghi calcoli, si ottiene facendo slittare i triangoli lungo i loro cateti, formando un quadrato che ha per lato le loro quattro ipotenuse. Così facendo, al centro si formerà un quadrato più piccolo, di lato 1, che andrà semplicemente sottratto dall’area del quadrato grande di lato 3. Quindi:
3 * 3 = 9 (area quadrato grande)
9 – 1 = 8 (si toglie il quadrato centrale)
8 / 4 = 2 (area di un solo triangolo.

4. Scudo-elica. Ogni quadretto ha per lato 1 cm. Determinare l’area della parte colorata.

4. SOLUZIONE. Due aree bianche si possono unire formando un cerchio tipo Yin Yang di raggio 1. In questo modo l’area bianca corrisponde a due cerchi di raggio 1, in totale [2(r²π)] ed è equivalente all’area del semicerchio di raggio 2, visibile in basso nella figura, [(2r)²π/2]. Infine, l’area colorata corrisponde al rettangolo 4 * 2 = 8 cm².   

5. Area colorata. Determinare l’area verde.

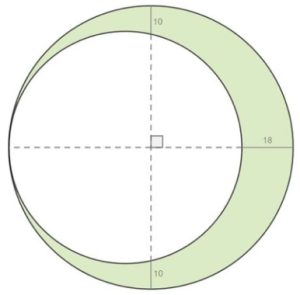
5. SOLUZIONE. Indicando con R il raggio del cerchio grande e con r il raggio del cerchio piccolo abbiamo:

1. 18 + 2r = 2R
2. 2R – 20 = C
3. R : C/2 = C/2 : (R-18) applicando il secondo Teorema di Euclide

Svolgendo la 2:  C/2 = R – 10. Sostituendo nella 3 otteniamo: (R – 10)² = R² – 18R; che diviene 2R = 100 quindi R = 50. Ora sostituendo nella 1 abbiamo: 18 + 2r = 100 quindi r = 41.  Infine area verde = R²π – r²π = 819π = 2.572.

A lunedì prossimo.