
Le soluzioni dell’11 luglio 2022 a cura di Fabio Ciuffoli
Ieri abbiamo proposto quattro giochi tratti dal libro “Con la testa fra le nuvole?” sottotitolo “Il mestiere del matematico” di Angelo Guerraggio e ora presentiamo le soluzioni.
Con la testa fra le nuvole? Il mestiere del matematico – soluzioni
1. Il costo di un CD. Aldo vuole acquistare un CD, ma non ha molto denaro, in particolare gli mancano 47 euro. Carla ha più soldi di Aldo ma anche a lei, per lo stesso acquisto, mancano 2 euro. A questo punto decidono di mettere insieme i loro pochi soldi, sempre in numeri interi di euro, ma questo totale non è ancora sufficiente per l’acquisto. Quanto costa il CD in euro interi?
1. SOLUZIONE. Il costo di un CD. Trasformiamo le informazioni del testo in equazioni indicando con A e C gli euro posseduti rispettivamente da Aldo e Carla e con p il prezzo del CD, avremo:
Sommando membro a membro le due equazioni otteniamo:
A + C + 49 = 2p che diventa A + C = 2p – 49.
Ora sostituendo nella disuguaglianza, avremo: 2p – 49 < p, quindi p < 49.
D’altra parte, nel testo del problema si dice che a Aldo mancano 47 euro, perciò il prezzo deve essere maggiore di 47. Le due disuguaglianze p < 49 e p > 47 portano a concludere che p = 48 euro. Il CD costa 48 euro.
2. Due professori e una bidella. Prodotto e Somma sono due professori di matematica che insegnano nella stessa scuola. Una bidella si diverte a provocarli con problemi di calcolo. Una mattina, con aria maliziosa, la bidella dice ai due professori: “Ecco la somma delle età delle mie due figlie” e rivolgendosi al professor Somma gli consegna un foglietto che il collega non può vedere. “Ecco il prodotto delle stesse due età” continua porgendo un altro foglietto solo al professor Prodotto. “Adesso fate vedere che siete dei bravi matematici e calcolate le due età, sapendo che le due figlie hanno almeno un anno”.
“A me il prodotto non basta” risponde il professor Prodotto. “Anch’io non posso rispondere” dice il professor Somma. La bidella li esorta dicendo “Sarete due esimi docenti di matematica, ma in questo momento mi state deludendo perché avete le informazioni necessarie per la soluzione del problema”
“Adesso io lo so, le due età sono…” dice il professor Prodotto.
Quali sono le età delle due figlie della bidella?
2. SOLUZIONE. Due professori e una bidella. Il professor Prodotto legge il prodotto delle due età, ma non è in grado di individuarle. Vuol dire che non ha letto un numero primo, altrimenti se avesse letto ad esempio 7 o 13 avrebbe potuto concludere che le due età sarebbero rispettivamente di 1 e 7 oppure di 1 e 13 anni.
Il professor Somma non ha letto 2 altrimenti il risultato sarebbe stato 1 e 1, mentre il professor Prodotto avrebbe letto 1 e quindi sarebbe stato in grado di concludere.
Il professor Somma non ha letto 3 che corrisponderebbe alle età 1 e 2, mentre il professor Prodotto avrebbe letto 2 che è un numero primo.
Il professor Somma non ha letto neppure 4 che corrisponderebbe a:
Dunque la somma scritta sul foglietto è maggiore o uguale a 5.
Il professor Somma potrebbe aver letto 5 che corrisponderebbe a 4 e 1 oppure a 3 e 2; potrebbe aver letto 6 che corrisponderebbe a 5 e 1 oppure 4 e 2 o anche a 3 e 3; potrebbe aver letto 7 che corrisponderebbe a 6 e 1 oppure a 5 e 2 oppure a 4 e 3 e via di seguito. All’aumentare della somma le possibili combinazione di due addendi aumentano, così come le possibili combinazioni dei due fattori e questo ci allontana dall’unicità della soluzione.
Il professor Prodotto ne diventa consapevole quando il suo collega dichiara di non saper rispondere ed a questo punto dichiara di poter risolvere il problema.
Se il problema, come affermato dalla bidella, ha un’unica soluzione possibile vuol dire che il prodotto delle due età si può scomporre in due fattori in più modi e la somma dei fattori di una di queste scomposizioni è un numero inferiore a 5.
Il solo numero naturale che soddisfa queste condizioni è 4 che può essere dato da 4 x 1 oppure da 2 x 2. Abbiamo già escluso 2 e 2, per la mancata risposta del professor Somma, quindi non resta che 4 e 1.
Le età delle due figlie sono 4 anni e 1 anno.
3. Obiettivo: non perdere. A turno due giocatori prendono una delle nove tessere disposte su un tavolo e numerate da 1 a 9. Vince chi per primo raggiunge il valore 15 sommando tre delle sue tessere non necessariamente le prime.
![]()
Quale tessera dovrà prendere il secondo giocatore nella sua prima mossa per cercare di non perdere?
3. SOLUZIONE. Obiettivo: non perdere. Il gioco si può schematizzare utilizzando la seguente tabella 3 x 3 che riporta tutte le terne x, y, z di numeri interi compresi tra 1 e 9 per cui x + y + z = 15. Si tratta di un quadrato magico con costante magica uguale a 15. Se il primo giocatore sceglie un numero pari, ossia uno posto ai vertici del quadrato, per il secondo giocatore è sufficiente scegliere il 5. Il primo giocatore dovrà successivamente muoversi in orizzontale o in verticale e il secondo potrà sempre neutralizzarlo, come nel gioco del tris. Analoga situazione se il primo giocatore sceglie un numero dispari diverso da 5. Se invece il primo giocatore sceglie il 5, per il secondo è sufficiente scegliere un numero pari. Il primo giocatore si dovrà poi muovere in orizzontale, in verticale o lungo una delle due diagonali e il secondo avrà sempre la possibilità di neutralizzarlo.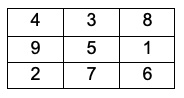
4. In bigiotteria. Il prezzo di tre anelli è uguale al prezzo di un braccialetto e quello di tre collane è uguale al prezzo di sette braccialetti. Se però si acquista un cofanetto di sette pezzi, che contiene almeno un anello, un braccialetto e una collana, si spenderanno 119 euro.
Quanto costa una collana?
4. SOLUZIONI. In bigiotteria. Indichiamo con a, b e c rispettivamente i prezzi di un anello, di un braccialetto e di una collana. Avremo:
3a = b e inoltre 3c = 7b.
Ora indichiamo con x il numero di anelli, con y il numero di braccialetti e con z il numero di collane presenti nel cofanetto, avremo
x + y + z = 7 e inoltre ax + by + cz = 119
ora andando a sostituire:
(b/3)x + by + (7/3)bz = 119
raccogliamo b, svolgiamo e scomponiamo 119 in 7 *17:
b(x + 3y + 7z)/3 = 7 * 17
Ne segue che b deve essere un multiplo di 3 poiché i numeri devono essere interi.
Ipotizziamo sia 3, ma x + 3y + 7z, dove x, y e z hanno ciascuno valore massimo 5, non può raggiungere il valore 119. Non può essere neppure b = 3 * 17 perché dovrebbe risultare x + 3y + 7z = 7 mentre già x + y + z = 7, e neppure b = 3 * 7 * 17.
Deve quindi essere b = 3 * 7 = 21. A questo punto il prezzo di una collana deve essere 3c = 7 * 21 dove c = 49 euro.
Una collana costa 49 euro.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
4 risposte
Sono felice di aver compreso a fondo il problema 3!
Perfetto! 👍
Segnalo il commento di Marco Rinetti al problema 3 e lo ringrazio per la partecipazione.
“Consideriamo un quadrato magico 3×3, visibile in figura. Il gioco qui descritto equivale a una partita a tris su tale quadrato, quindi occorre seguire le strategie vincenti del tris (posto che esiste sempre un modo, per entrambi i giocatori, di forzare la patta).
– Con ogni probabilità, il primo giocatore nella sua prima mossa pescherà il 5. In tal caso il secondo giocatore dovrà pescare un numero pari per garantirsi la patta.
– Se il primo giocatore dovesse pescare un numero pari, il secondo giocatore deve necessariamente pescare il 5, perché in caso contrario il primo giocatore ha una strategia vincente.
– Se il primo giocatore dovesse pescare un numero dispari diverso dal 5, il secondo giocatore dovrà scegliere o 5 o un numero pari, altrimenti il primo giocatore ha di nuovo una strategia vincente.”
Segnalo due proposte di soluzione del problema 2. Due professori e una bidella, che trovo particolarmente chiare e interessanti.
Fabio DF: “La prima risposta del prof Prodotto ci fa eliminare tutte le coppie che hanno un prodotto univoco. La risposta del prof. Somma ci fa eliminare tutte le coppie che, tra quelle rimaste dopo il primo passaggio, hanno una somma univoca.
A questo punto, il prof. Prodotto è in grado di stabilire le due età, per cui, tra quelle rimaste, bisogna scegliere quelle che hanno prodotto unico.
In particolare, il prof. Prodotto, all’inizio, avendo avuto come indizio 4, ha le due possibilità (1, 4) e (2, 2). In particolare, scarta la coppia (1,3) che è l’unica ad avere come prodotto 3 (in questo caso, avrebbe indovinato subito). Ma se fosse stata la coppia (2, 2), il prof Somma avrebbe avuto come indizio 4, ed avrebbe indovinato subito, essendo l’unica coppia rimasta con somma 4. Non essendo questo il caso, la coppia (2,2) è scartata, ed il prof. Prodotto riesce ad individuare le due età che sono 1 e 4.”
Antonio Santorsola: “1-1, 1-2, 1-3, 1-5, 1-7 … sono coppie da scartare altrimenti il prof. Prodotto avrebbe indovinato subito. Il prof Somma lo sa, ma non ha comunque una soluzione univoca. Le somme da escludere sono certamente 2 e 3. Se sul fogliettino di Somma ci fosse scritto 4, Somma escludendo 1-3 avrebbe la soluzione 2-2 ma, dichiarando di non averla, si può escludere la somma 4. Ipotizziamo la somma 5, le possibilità per il prof. Somma sono 1-4 e 2-3. Il prof Prodotto esamina le due possibili coppie che danno somma 5. In più sappiamo dalla bidella che c’è una soluzione univoca. 2-3 è da escludere perché il prodotto 6 ha anche la coppia 1-6. Rimane 1-4 che è la soluzione. Il prof. Prodotto avendo in mano il biglietto con il numero 4 ed escludendo la coppia 2-2 può dare una soluzione univoca. Le figlie hanno 1 e 4 anni.”
Ringrazio Antonio Santorsola e Fabio DF per la partecipazione.