
I giochi del lunedì di Prisma del 31 gennaio 2022 a cura di Fabio Ciuffoli
Oggi proponiamo cinque giochi che prevedono diversi metodi per la soluzione, indicativamente un metodo privilegia l’approccio visivo e l’altro quello del calcolo. Invitiamo i lettori a inviarci osservazioni e proposte di soluzione utilizzando lo spazio riservato ai commenti. Alle ore 17.00 di domani pubblicheremo le soluzioni con i procedimenti.
Affidarsi agli occhi e affidarsi ai conti
1. ABC è un triangolo rettangolo dove l’ipotenusa AC è il diametro della circonferenza più grande. I cateti misurano 8 cm e 15 cm. Quanto vale la somma dei diametri delle due circonferenze?
2. L’area del quadrato è 225 cm2 divisa in nove quadratini uguali tra loro. La stella è stata costruita congiungendo i vertici del quadrato con i punti medi dei lati del quadratino centrale. Quanto vale l’area della stella?
3. Quanto vale l’area del quadrato grigio, sapendo che l’area del quadrato a puntini è un quarto dell’area del quadrato grande?
4. All’interno del quadrato in figura è stato disegnato un triangolo. Qual è il rapporto tra l’area del triangolo e l’area del quadrato?
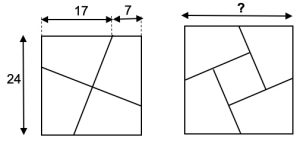
5. Il puzzle, in figura a sinistra di chi legge, è stato costruito dividendo un quadrato di lato 24 cm con due segmenti perpendicolari tra loro e passanti per il centro del quadrato. I quattro pezzi del quadrato così ottenuti possono essere assemblati di nuovo per formare l’altro quadrato, con un buco nella regione centrale, a destra in figura. Quanto misura in cm il lato del nuovo quadrato?
 Disegno non in scala
Disegno non in scalaAggiornamento per le soluzioni click qui
I giochi presentati oggi sono stati tratti da un articolo pubblicato sulla prima uscita di Prisma N. 1 ottobre 2018 e il conseguente dibattito e confronto.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
27 risposte
1 Essendo l’ipotenusa del triangolo ABC il diametro del cerchio grande,applicando il teorema di Pitagora si ottiene 17 cm.
A occhio il diametro del cerchio piccolo mi sembra che corrisponda alla metà del cateto più lungo…7.5cm.
Somma dei diametri 24.5 cm.
2 Ho calcolato il lato del quadrato..15 cmq,ho calcolato l’area della parte colorata…15×5÷2×4=150 cmq..infine
225_150=75 cmq area della stella.
3 Area del quadrato grande..225×4=900cmq
Area del triangolino in alto,a destra,
900÷18=50cmq
Area del quadratino..50×4= 200cmq.
4 Il rapporto è 3/8.
5 17 _7=10cm
10×10=100 cmq
24 X 24= 576 cmq
576+100=676
Radice quadrata di 676…26 cmq
Il primo non è corretto, gli altri vanno benissimo. Ricordo che per ogni problema ci sono due o più metodi di soluzione. A domani per le soluzioni
Nel quesito 5 , prima calcolo i lati dei quadrilateri uguali della prima figura e trovo: 13; 13; 7; 17. Poi osservo che nella seconda figura il lato è ottenuto accostando due lati uguali “medi” dei quadrilateri: 13 +13 = 26.
Ottimo, domani le soluzioni con disegni e descrizione.
Soluzione “visiva” al quesito 4. Tracciando diagonali e assi dei lati, i due triangoli grigi che fanno parte della figura dall’area ricercata sono equivalenti ai due triangoli blu in basso a destra. L’area è quindi uguale al quadrato in basso a destra più metà quadrato in alto a sinistra(colorata anch’essa in blu): 1/4 Q + 1/8 Q = 3/8 Q. Il rapporto vale quindi 3/8.
Ottimo a domani per le soluzioni con tutte le dimostrazioni
Bella dimostrazione, a domani per le soluzioni con tutte procedure.
Soluzione quesito 1
Propongo una nuova soluzione al primo quesito che mi sembra più elegante.
Hai colto l’obiettivo dei giochi presentati oggi!
5) Pardon, ho sbagliato, il nuovo lato del quadrato è 26 cm
=2* sqrt(12^2 + (17-12)^2) = 26 cm
Con questa ultima correzione, è tutto perfetto. Hai utilizzato il metodo dei conti, se ha voglia gli stessi risultati li puoi ottenere utilizzando l’intuizione visiva, quasi senza far di conto. A domani per le soluzioni.
1) AC = sqrt(8^2+15^2) = 17 cm
Area ABC = 8*16/2 = 60 cm^2
Perimetro ABC = 15+8+17 = 40 cm
Raggio cerchio piccolo = 60*2/40 = 3 cm
Somma dei due diametri = 17 è 6 = 23 cm
2) Area della stella = 225 – 4*(15*5)/2 = 75 cm^2
3) Area quadrato grigio = (20*20)/2 = 200 cm^2
4) Rapporto area triangolo/area quadrato = [L^2 – L^2(1/8+2*1/4)]/L^2 = 3/8
5) ? = sqrt(24^2 + 7^2 ) 25 cm
Quesito 1: AC²=AB²+BC² da cui AC=17 cm=diametro circonferenza circoscritta. L’area del triangolo vale 8×15/2 cm² = 60 cm². Suddividendo il triangolo in 3 triangolini con un lato uguale ad uno del triangolo di partenza e come terzo vertice il centro della circonferenza, si nota come la somma delle aree dei tre triangolini sia uguale a quella del triangolo di partenza. Si può facilmente calcolare r = raggio della circonferenza inscritta eguagliando la somma delle aree a 60 cm² e si ricava che r=3 cm da cui d=6 cm. La somma dei diametri vale in definitiva 17 cm + 6 cm = 23 cm.
Bellissima dimostrazione. Se hai voglia e tempo puoi cercare anche un altro metodo, diciamo visivo, per arrivare al risultato.
Nel Secondo quesito, l’area della stella centrale è 75 cm²?
Ottimo. Domani pubblicheremo tutte le soluzioni con dimostrazione.
Per quanto riguarda il quesito 5, il quadratino al centro del quadrato di destra ha il lato che misura (17-7) cm, come si nota analizzando la disposizione dei lati dei quadrilateri a partire dalla figura a sinistra. L’area della figura a destra è dunque 100 cm² (area del quadratino al centro) + 576 cm² (area della figura a sinistra che è solo riorganizzata e dunque non cambia area) = 676 cm².
Ottimo, anche se manca l’ultima operazione. Il problema chiede di calcolare il lato del nuovo quadrato.
Pardon, il lato ovviamente è la radice quadrata di 676 cm² cioè 26 cm.
La mia soluzione al quesito 2 – tracciando le diagonali si nota che l’area della stella è 4 volte la differenza tra un qualsiasi triangolo rettangolo isoscele tracciato dalle diagonali (con area 1/4 del quadrato = 1/4 Q) e un qualsiasi triangolo isoscele che ha per base il lato del quadrato e per altezza 1/3 del lato.
Ottimo
Credo che la risposta del terzo esercizio dipenda dall’angolazione del quadrato grigio, se è posizionato a 45° l’area vale 200 cm²
Il quadrato grigio ha “un’angolazione” di 45° rispetto al quadrato grande.
Grazie mille! Chiedo scusa per il linguaggio poco formale dal punto di vista matematico ma ho scritto di fretta perché stavo per entrare a scuola!
Quesito 4: l’area del triangolo interno è data dall’area del quadrato – (l’area del triangolo in alto a sinistra + l’area di quello a destra + l’area di quello in basso). Area del triangolo in alto a sinistra = 1/2 × 1/2 l × 1/2 l = 1/8 Q. Area del triangolo a destra = area del triangolo in basso = 1/2 × 1/2 l × l = 1/4 Q. La somma vale 5/8 Q e quindi l’area del triangolo interno vale Q – (5/8 Q) = 3/8 Q e il rapporto tra la sua area e quella del quadrato vale (3/8 Q)/Q = 3/8.
Ottimo, c’è anche una dimostrazione grafica, senza fare “conti”. I Giochi di oggi, come suggerisce il titolo, vogliono evidenziare che sono possibili più metodi di soluzione.