
Le soluzioni dell’1 novembre 2021 a cura di Fabio Ciuffoli
Wasan l’arte dei numeri giapponese
Ieri mattina abbiamo proposto due giochi prendendo spunto dalla matematica Wasan. Presentiamo ora le soluzioni.
1. Sono stati preparati cinque dolci di riso noshimochi uguali a forma rettangolare. Tre vengono disposti orizzontalmente e due verticalmente, come in figura. La somma dei lati a destra è 87 sun. Sapendo che il lato lungo di ogni dolce è 21 sun, determinare la lunghezza del lato corto. (Il sun è un’unità di misura giapponese che corrisponde a 3 cm circa).
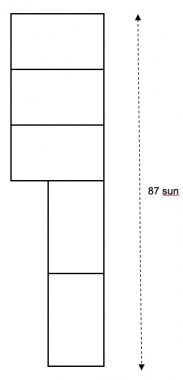
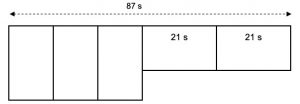
Chiamiamo A la lunghezza del lato corto, avremo:
3A + 21 * 2 = 87 da cui 3A + 42 = 87 poi 3A = 45 infine A = 45/3 = 15 sun.
2. Durante le feste di shogatsu, il capodanno giapponese, i bambini giocano facendo rimbalzare le sfere temari. Al primo tentativo la temari viene fatta rimbalzare 9 volte. Al secondo tentativo, 23 volte. Al terzo tentativo, 45 volte e al quarto, 75 volte. Se il numero dei rimbalzi continua a crescere con questo ritmo, qual è il numero dei rimbalzi all’ottavo tentativo? Inoltre quanti tentativi sono necessari per arrivare a 423 rimbalzi?
2. SOLUZIONE. Organizziamo le informazioni e cerchiamo uno schema ricorrente. Osserviamo gli intervalli tra i numeri
Osserviamo gli intervalli tra i numeri
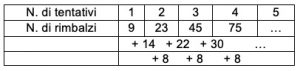
A ogni tentativo successivo, il numero dei rimbalzi aumenta di 14, 22, 30 e via di seguito, mostrando un incremento regolare di 8. Ora, ampliando lo schema fino all’ottavo tentativo, si ottiene il risultato richiesto di 275. Infine osserviamo che 423 rimbalzi si raggiungono al decimo giorno. I risultati sono evidenziati in grassetto.

Osservando la tabella, si può trovare la funzione che mette in relazione il numero di tentativi con il numero di rimbalzi. Vi sono diversi metodi per individuare questa funzione, alcuni ben illustrati dai nostri lettori. Chiamando n il numero di tentativi e R il numero di rimbalzi avremo: 9 + (2n – 2) (2n + 3) = R che diviene 4n2 + 2n + 3 = R. Ora sostituendo n con 8, otteniamo 275 rimbalzi; sostituendo R con 423 e risolvendo l’equazione di secondo grado, otteniamo 10 tentativi.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
2 risposte
Ecco le formule proposte da Alessandro Pettinelli:
Tra le soluzioni proposte vorrei segnalare il commento di Andrea. Ottimo procedimento, ben articolato e con soluzione. Definendo n il numero di tentativi e R il numero di rimbalzi, individua la funzione
4n * (n + 1) – 2 n + 3 = R che sviluppata porta allo stesso risultato esposto sopra.
Molto interessante la soluzione proposta da Alessandro Pettinelli, che riporto di seguito. Si articola in due formule. La (1) che ha validità per numero di ribalzi superiore a 2; e la (2) che ha validità generale.
Definendo xn il numero di rimbalzi all’ennesimo tentativo e n il numero di tentativi avremo le seguenti due formule.
Scrive Alessandro: “La (1) mi è venuta in mente osservando che xn – xn–1 = xn–1 – xn– 2 + 8 ovvero che il delta tra due elementi della successione aumenta di 8 ad ogni volta che n aumenta di 1. La (2) è chiaramente più esplicativa ma più difficile da desumere direttamente, almeno per me.”