
Le soluzioni del 13 settembre 2021 a cura di Fabio Ciuffoli
Nella prima mattinata di ieri abbiamo proposto tre problemi e ora presentiamo le soluzioni.
Gli enigmi colorati di Catriona – soluzioni
1. Spicchi arancioni. Se il raggio di ogni semicerchio è 5 cm, qual è l’area ombreggiata in giallo totale?
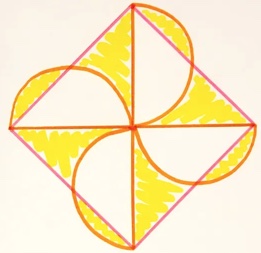
1. SOLUZIONE. Se riorganizziamo l’immagine e l’ombreggiatura, come proposto in figura, i quattro triangoli ombreggiati formeranno il quadrato che ha come lato il diametro di ogni semicerchio, 10 cm. Quindi l’area totale è 100 cm2.

2. Doppia spirale. Dieci punti, equidistanti 4 cm l’uno dall’altro, sono uniti da semicerchi e formano la seguente spirale. È maggiore l’area rossa o arancione? E di quanto?
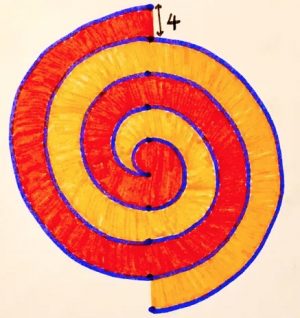
2. SOLUZIONE. Area rossa maggiore di 4π cm2. L’intuizione qui è immaginare di tagliare la spirale lungo la linea blu e spostare il lato destro verso l’alto di 4 cm.
Avremo così sezioni corrispondenti, su entrambi i lati della linea blu, tranne al centro dove c’è un piccolo cerchio di raggio 2 cm, disegnato in nero e giallo, con area rossa. Abbiamo quindi più rosso che arancione, esattamente di 22π = 4π cm2.
3. La ciambella rosa. I quattro punti, sulle due circonferenze, sono equidistanti di 2 cm. Qual è l’area ombreggiata?
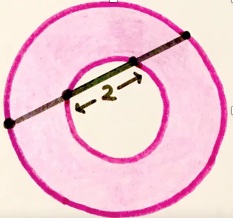
3. SOLUZIONE. 8π cm2.Il problema non specifica la posizione dei punti sulle circonferenze. Supponiamo che non sia rilevante e quindi spostiamoli in un punto conveniente, come il diametro.
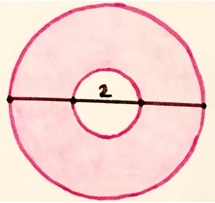
Diviene evidente che l’area ombreggiata è la differenza tra un cerchio di raggio 3 e un cerchio di raggio 1, che è π32 – π12= 8π cm2.
Tuttavia, possiamo anche usare il teorema di Pitagora per mostrare che non importa dove sia la linea. Se la linea non passa per il centro, crea due triangoli ad angolo retto come di seguito.
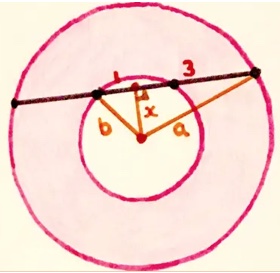
Un ulteriore metodo per la soluzione è l’utilizzo del teorema delle corde, illustrato da Daniele nel suo primo commento.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
Una risposta
I deliziosi puzzles geometrici di Catriona Shearer sono molto seguiti da studenti, insegnanti e appassionati, anche per la loro fruibilità. Infatti sono particolarmente adatti per la diffusione via Twitter usando “solo” 280 caratteri + una figura!