Menu
I giochi del lunedì di Prisma del 15 novembre 2021 a cura di Fabio Ciuffoli
I giochi che proponiamo oggi sono ispirati agli esperimenti ideati dallo psicologo cognitivo inglese Peter Wason risalenti a più di 50 anni fa, ma ancora straordinariamente attuali. Presentiamo tre problemi, sotto forma di gioco e invitiamo i lettori a inviarci osservazioni e proposte di soluzione nello spazio riservato ai commenti. Alle ore 17.00 di domami pubblicheremo le soluzioni argomentate e corredate dalla descrizione dell’esperimento originario.
Il compito di selezione
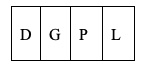
1. Quattro carte, che riportano su entrambi i lati una lettera dell’alfabeto, sono disposte nel seguente modo. Quante occorre girare per verificare l’affermazione: “Dietro ogni G si trova una L”?
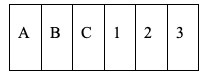
2. Sei carte, ciascuna delle quali su un lato porta scritto una fra le lettere A, B, C e sull’altro porta scritto una fra le cifre 1, 2, 3, vengono disposte su un tavolo in questo modo.
Quali carte è necessario girare per determinare la verità dell’affermazione: “Se una carta porta la lettera B su un lato, allora sull’altro lato porta la cifra 2”?
3. In un mazzo di carte, su ogni carta sono segnati due numeri, uno su ogni faccia e dietro ogni numero pari c’è un multiplo di 3. Quale di queste 5 affermazioni è vera?
A) una carta può contenere 3 su un lato e 5 sull’altro;
B) nessuna carta può avere su un lato un numero doppio di quello che c’è sul lato opposto;
C) se su un lato c’è 15, sull’altro lato non ci può essere 7;
D) nessuna carta può avere lo stesso numero su entrambi i lati;
E) ci può essere una carta che contiene 11 su un lato 18 sull’altro.
Aggiornamento per le soluzioni click qui
I problemi presentati oggi sono rielaborazioni aggiornate del Card Test presentato in Reasoning – New horizons in psychology di Peter Cathcart Wason. In copertina A three-color confetti illusion with spheres, which appear to be yellowish, reddish, and purpleish but in fact have exactly the same light-brown base color (RGB 255,188,144) di David Novick.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
3 risposte
Riporto due interessanti procedimenti di soluzione del problema n. 2.
Il primo è stato scritto da Fabrizio Garrucciu.
La premessa dice (dal punto di vista strettamente logico-grammaticale) che se una carta riporta su un lato la lettera B, allora sull’altro ha il 2: il che equivale a premettere che tutte le carte con la B hanno il 2 sull’altro verso: ciò che smentirebbe la premessa sarebbe trovare la lettera B sul verso opposto delle carte riportanti i numeri 1 e 3. Non ci importa invece che altre carte riportanti il numero 2 possano riportare sull’altro verso una lettera diversa da B (tale circostanza infatti non contraddirebbe la premessa). Pertanto, per confermare la premessa è necessario e sufficiente voltare la carta con la lettera B e le carte con i numeri 1 e 3.
Il secondo è stato scritto da Arturo De Biasi
Almeno B.
Non c’è il 2… ci fermiamo
C’è il 2… occorre una verifica.
Giriamo la 1…
C’è una B ? Ci fermiamo : falso
Non c’è una B ? … occorre altra verifica
Giriamo la 3…
C’è una B ? : falso
Non c’è una B ? L’asserzione è vera.
Quindi : da 1 a 3 carte.
Io dico 1. Tre carte
2. Girare B, 1, 3
3. La affrmazione vera é la A
Aspetto soluzioni
Bene, a domani per le soluzioni argomentate.