L’infinito tra matematica e fisica

“Sempre caro mi fu quest’ermo colle,
e questa siepe, che da tanta parte
dell’ultimo orizzonte il guardo esclude”

Nel verso iniziale de “L’infinito”, Leopardi suggerisce che il concetto di infinito sia legato all’immaginazione; infatti, non sono gli spazi aperti in cui lo sguardo può perdersi lontano a ispirare al poeta l’idea d’infinito, bensì una siepe che impedisce la vista e che obbliga la fantasia a pensare all’oltre. Anche per i matematici l’immaginazione è molto importante e spesso, grazie a bizzarri stratagemmi mentali, riescono a formulare intricate teorie. Per il concetto di infinito ne è un esempio il paradosso del Grand Hotel, ideato dal matematico David Hilbert durante alcune lezioni divulgative degli anni Venti del XX secolo e reso popolare da un libro di G. Gamow del 1947. Dapprima si immagina un hotel con infinite stanze, tutte occupate, e poi suppone che arrivi un nuovo singolo ospite e si chiede se potrà essere ospitato in questo hotel. La risposta è affermativa, in quanto basterà semplicemente spostare tutti i clienti nella camera successiva infatti, benché l’albergo sia pieno, essendo infinito è comunque possibile sistemare il nuovo ospite. Poi immagina che arrivino infiniti nuovi ospiti e anche in questo caso riesce a sistemarli, infatti, basterà spostare ogni ospite nella stanza con numero doppio rispetto a quello precedente lasciando ai nuovi arrivati tutte le camere con i numeri dispari.

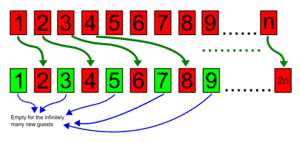
Da questo paradosso se ne può creare facilmente un altro. Immaginiamo una persona che esamini l’ordine di ciascuna camera: ipotizzando che ci impieghi 1 minuto per la prima e un tempo che si dimezza per ogni camera successiva, avrebbe impiegato 2 minuti per esaminare un hotel di infinite camere il che ovviamente è insensato. E se ora ci chiedessimo dove si trova alla fine dell’ispezione questa persona? È impossibile rispondere, ma questa domanda esula dall’immaginazione e ci riporta nel reale che al matematico “piace” meno.

Dopo la visualizzazione di questo problema a livello creativo, per un matematico diventa affascinante dedurre una teoria. Si deve a Georg Cantor a fine ‘800 la formalizzazione con rigore matematico di un concetto di portata filosofica come l’infinito.

Aristotele aveva fatto la distinzione fra infinito in atto (o “attuale”) e infinito in potenza (o “potenziale”): con l’espressione infinito potenziale egli intendeva la possibilità di aggiungere sempre qualcosa a una quantità determinata senza che ci fosse mai un elemento ultimo, quindi come qualcosa che può essere sempre ulteriormente diviso o esteso, ma mai completamente realizzato. Diversamente, l’infinito attuale era inteso come collezione infinita, compiutamente data, di tutti i punti di un insieme geometrico; pertanto, è un infinito che esiste in una forma completa e realizzata.

I matematici avevano sempre preferito parlare di “infinito potenziale” fino a Cantor che introdusse l’infinito attuale a partire da un nuovo modo di intendere la matematica, la teoria degli insiemi. Il frutto del suo lavoro è la formulazione di concetti contrari all’intuizione, come il fatto che non tutti gli insiemi infiniti hanno la stessa cardinalità, ma che esiste un’intera gerarchia infinita di infiniti che diventano sempre più grandi. Infatti l’insieme dei numeri reali non è numerabile perché non può essere messo in relazione biunivoca con l’insieme dei numeri naturali e ha la stessa cardinalità dell’insieme dei punti del piano e dell’insieme dei punti dello spazio tridimensionale. L’ardire costò caro a Cantor: le sue idee suscitarono un furibondo rifiuto da parte di molti suoi contemporanei, circostanza che fu probabilmente la causa scatenante della pazzia che lo condusse alla morte.

Fu David Hilbert a riconoscere il valore delle idee di Cantor che ai suoi detrattori rispose: “L’opera di Cantor è il prodotto più bello del genio matematico e uno dei progressi supremi dell’attività umana puramente intellettuale. Nessuno potrà scacciarci dal paradiso creato per noi da Cantor.”

Nella realtà, però, siamo abituati a ragionare in termini di serie di numeri finiti di cose che, seppure piccolissimi o grandissimi, sono comunque diversi dall’infinito. Per esempio, è proprio di pochi giorni fa la scoperta del più grande numero primo di Marsenne 2^136.279.840 – 1, un numero composto da 41.024.320 cifre, eppure in confronto all’infinito sarebbe comunque nulla.

Sebbene, quindi, l’infinito non si comporti come nulla di tutto ciò che conosciamo in Natura, per i matematici esiste senza ombra di dubbio, esiste un simbolo per esprimerlo e metodi per manipolarlo che danno risultati condivisibili permettendo di risolvere problemi pratici. L’infinito crea invece seri problemi alla fisica, per esempio quando la curvatura dello spazio-tempo tende ad un valore infinito si ha una singolarità gravitazionale, in cui tutte le leggi della fisica ad oggi conosciute non valgono più.

I fisici, al contrario dei matematici, si chiedono se l’infinito esista veramente in Natura o non sia solo frutto della mente umana, se lo spazio-tempo sia realmente infinito e se l’infinito si possa circoscrivere e quindi misurare. La fisica attuale è propensa a ritenere che l’infinito non esista realmente in Natura, che lo spazio non sia davvero continuo e che non possa essere diviso all’infinito. Il filosofo Anassimandro sosteneva che era opportuno postulare, immaginare, l’esistenza di qualcosa, che chiamò “apeiron”, che non era nessuna delle sostanze del mondo conosciuto dall’esperienza, ma che fungeva da elemento unificante per spiegare tutte le cose. In questo modo poteva immaginare la realtà come formata da entità non visibili, ma che rendono conto dei fenomeni.
Dopo di lui, Democrito chiamò “atomos” gli elementi su cui veniva costruita ogni cosa ed era importante definire che essi non potessero essere divisi all’infinito in parti sempre più piccole. Questi atomi dovevano anche essere solidi, compatti, non uguali tra loro ed eterni perché niente poteva essere creato dal niente in accordo con quanto sostenuto dagli eleati. Democrito sosteneva che in Natura esisteva un numero infinito di atomi dotati di forme diverse in modo da potersi unire per formare corpi diversi e che anche l’anima era costituita da atomi rotondi e lisci che, dopo la morte, si sarebbero sparsi in ogni direzione dando vita a una nuova anima.
Oggi sembra che l’intuizione di Democrito fosse corretta: la fisica ha scoperto che gli atomi sono composti da particelle ancora più piccole, ma concordano nell’affermare che ci debba essere un limite minimo.
Questo concetto è alla base della teoria della gravità quantistica che tenta di fornire un quadro teorico unitario tra la teoria della relatività generale, la nostra migliore teoria attuale della gravità, che modella la struttura dell’Universo su scala macroscopica, e la teoria della meccanica quantistica, che descrive i fenomeni tipici della scala atomica e subatomica.
L’idea di Rovelli, che ha dato un grandissimo contributo nella teoria della gravità quantistica a loop, è che lo spazio sia fatto di quanti di gravità che hanno un volume minimo, citando le sue parole, dal libro “La realtà non è come ci appare”, “…lo spazio è un pullulare di grani che interagiscono tra loro e con le cose. Lo spazio è creato dall’interagire di quanti individuali di gravità”.