L’equazione che mandò l’uomo sulla Luna

Nella rubrica “Topics of the Times”, sul New York Times del 13 gennaio 1920, un ignoto ma caustico autore, nel commentare una nuova teoria sul volo di razzi nello spazio, affermava: “Sarebbe assurdo dire che il professor Goddard, con la sua cattedra al Clark College e l’approvazione dello Smithsonian Institution, non conosca il principio di azione e reazione e la necessità di avere qualcosa di più del vuoto contro cui reagire. È solo che gli mancano le nozioni impartite quotidianamente alle scuole superiori”. Chi era questo professor Goddard e quale la sua colpa per meritare questa stroncatura e sostanziale dichiarazione di incompetenza da parte di un autorevole giornale? Era vero che non conoscesse il principio di azione e reazione, noto anche come il terzo principio della dinamica di Newton? E, soprattutto, perché si parlava di razzi spaziali nel 1920, un’epoca che aveva da poco visto l’inizio del volo atmosferico con aeroplani e dirigibili? In effetti, sarà solo nell’ottobre del 1942 che si riuscirà a lanciare un oggetto fuori dall’atmosfera: purtroppo sarà il prototipo delle famigerate V2 progettate per Hitler dal barone Werner von Braun, la cui genialità ingegneristica nel realizzare razzi spaziali sarà poi al servizio degli americani durante la guerra fredda. Sarà lui a progettare il Saturn 5 che porterà l’uomo sulla Luna! Von Braun non era un teorico e i suoi progetti utilizzavano una scienza dei razzi (rocket science in inglese, un termine che indica per antonomasia una teoria complicatissima) venuta prima dei razzi, esattamente come la scienza dei calcolatori è venuta prima dei computer. La prima teoria del volo spaziale si può far risalire tra il 1810 e il 1813, con la pubblicazione degli articoli scientifici di William Moore, un personaggio misterioso del quale si ignora persino la data di nascita e che insegnava matematica all’Accademia militare di Woolwich, in Inghilterra. Presto dimenticata, toccò a un altro personaggio singolare e affascinante, vissuto nella Russia di inizio ‘900, Konstantin Ėduardovič Ciolkovskij, riscoprire la teoria dei razzi. Ingegnere, scienziato, filosofo, scrittore e completamente autodidatta, Ciolkovskij, grande ammiratore di Jules Verne, immaginava un avvenire di colonizzazione spaziale per l’umanità e lo descrisse nelle sue opere filosofiche e di fantascienza. A corredo di queste sue teorie visionarie, Ciolkovskij riscoprì la teoria del volo spaziale, giungendo a un’equazione analoga a quella di Moore, che metteva in relazione la velocità che un razzo può raggiungere nello spazio con i parametri strutturali del razzo stesso. Le idee dell’eccentrico e isolato Ciolkovskij non filtrarono in occidente ma la formula fu riscoperta poco appresso da un altro pioniere dell’era spaziale, proprio quel professore che il New York Times insinuava non conoscesse nemmeno la fisica delle superiori: Robert Goddard. Questi, nel 1914, aveva depositato due brevetti che proponevano di usare propellenti liquidi e di segmentare i razzi in più stadi. Idee messe poi in pratica da Von Braun e che hanno permesso all’uomo di raggiungere la Luna. L’equazione del razzo, scoperta e dimenticata dunque più volte come una fenice matematica, è la seguente:

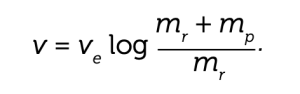
Potrebbe sembrare a prima vista incomprensibile (d’altra parte è rocket science…) ma in realtà è facile spiegarne i termini e quindi anche il significato. A primo membro troviamo v, la velocità che il razzo può raggiungere consumando tutto il suo carburante, mentre a secondo membro figura v_e cioè la velocità con cui il propellente del razzo viene espulso dal razzo durante il suo volo. Nei video dei lanci spaziali vediamo sempre che il razzo ha in coda uno sbuffo rovente, che è proprio il propellente consumato nel dare la spinta al razzo che fuoriesce dalla sua base. La parola log vuol dire logaritmo ed è un’operazione che applicata a una quantità x che aumenta in modo esponenziale, la fa crescere in modo lineare: in pratica, y = log x significa che y cresce molto più lentamente di x. Infine, m_p è la massa del carburante e m_r la massa del razzo con il serbatoio vuoto (cioè senza carburante): la massa totale a serbatoio pieno è m_r + m_p (si noti che per applicare l’equazione non è necessario conoscere m_p e m_r ma solo il rapporto (m_r + m_p)/m_r). L’equazione del razzo afferma dunque che che il rapporto (m_r+m_p)/m_r cresce esponenzialmente rispetto al rapporto v/v_e: ciò vuol dire che, al crescere della velocità massima v che possiamo raggiungere con il razzo, il rapporto fra la massa del carburante e quella del razzo deve aumentare in modo esponenziale. Per questo motivo, i razzi spaziali sono per la maggior parte fatti da carburante! Tanto per farsi una idea, se la massa del razzo è per l’85% data dal carburante, come nel caso dello Space Shuttle, allora il quoziente (m_r + m_p)/m_r è pari a (15+85)/15=100/15=6,7 (circa), il cui logaritmo fa circa 1,9: grazie all’equazione del razzo, la velocità che possiamo raggiungere con lo Shuttle consumandone tutto il carburante è pari a v = v_e×1,9. Poiché, per lo Shuttle, la stima di v_e è di 4 km/s, troviamo che la velocità raggiungibile dal razzo è all’incirca v = 4×1,9 = 7,6 km/s, cioè più o meno 27.000 chilometri l’ora! Nell’articolo al vetriolo del New York Times si menziona esplicitamente il principio di azione e reazione: se un corpo A esercita su un altro corpo B una azione data da una certa forza F_A e i due corpi restano fermi, vuol dire che B esercita su A una forza F_B di reazione della stessa intensità ma in direzione opposta a F_A, cioè F_A+ F_B=0. Per esempio, se due persone si trovano ai due lati di una porta e ciascuna prova a spingere la porta per aprirla esattamente con la stessa forza, la porta resterà ferma; se una delle due esercita una forza maggiore, la porta si aprirà nella direzione dell’altro. Il sillogismo del New York Times era quindi: un razzo si muove solo se ha un altro corpo sul quale esercitare una forza. Nell’atmosfera questo corpo è l’aria, ma nello spazio non c’è aria e dunque nello spazio il razzo non potrà mai muoversi. Eppure, abbiamo tutti visto satelliti e astronavi muoversi nello spazio! Come è possibile senza violare i principi di Newton? Per capire meglio la questione, chiediamoci cosa sia una forza. Ce lo dice il secondo principio di Newton, secondo il quale la forza di un corpo a un dato istante è il tasso di variazione della quantità di moto m×v del corpo (dove m ne è la massa e v la velocità). La quantità di moto di un corpo può cambiare da un istante all’altro e la velocità di questo cambiamento è la forza. Per due corpi in equilibrio, il terzo principio ci dice che la somma delle forze corrispondenti è zero e quindi non c’è alcuna variazione nella somma delle loro quantità di moto, che resta costante nel tempo. Attenzione che ora comincia la scienza dei razzi: continuino la lettura solo i cuori impavidi. Consideriamo un razzo nello spazio che nell’intervallo di tempo Δt espella una massa Δm di carburante imprimendole una velocità costante v_e. Se a un certo istante il razzo ha velocità v e massa m_r + Δm, passato l’intervallo di tempo Δt, la massa del razzo sarà diminuita a m_r, la sua velocità incrementata a v + Δv (dove Δv è una incognita) mentre la massa del propellente espulso è Δm e la sua velocità è v-v_e perché la sua velocità iniziale era v, la stessa del razzo (visto che ne faceva parte!), e la velocità di espulsione v_e va in direzione opposta a v. La quantità di moto totale del sistema deve rimanere costante prima e dopo questa espulsione: prima era data da (m_r + Δm)v (il carburante fa ancora parte del razzo); dopo, è data da m_r(v+Δv)+Δm(v- v_e), dove il secondo termine è la quantità di moto del carburante espulso nell’intervallo di tempo Δt. Uguagliando queste due espressioni, troviamo:

(m_r+Δm)v=m_r(v+Δv)+Δm(v-v_e) e, svolgendo i prodotti, m_r v + Δm v = m_r v + m_r Δv + Δm v – Δm v_e.

I termini m_r v e Δm v al primo e secondo membro si elidono e troviamo m_r Δv = Δm v_e cioè m_r=Δm v_e/Δv. Questa equazione ci dice quel che accade in un intervallo Δt di tempo: sommando tutti questi Δv per ciascun intervallino Δt, fra l’istante in cui il serbatoio è pieno e l’istante in cui il serbatoio è vuoto, si trova proprio la formula del razzo:

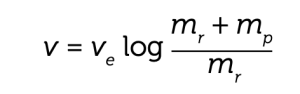
ma per questo serve un po’ di calcolo integrale che qui ci risparmiamo. Se tutto questo sembra difficile, lo è: del resto ci mandiamo i razzi sulla Luna! Per concludere, va detto che il New York Times ha rettificato il suo errore “appena” 49 anni dopo, nel 1969, quando il primo uomo ha messo piede sulla Luna. Nella rettifica non si nomina Goddard bensì si dichiara che i principi della dinamica di Newton sono stati confermati da quell’impresa. Hanno continuato a guardare il dito, invece della Luna.