Salviamo la geometria!

Qualche settimana fa abbiamo pubblicato su questo sito una interessante riflessione della professoressa Maria Dedò che, partendo dalla soluzione algebrica – più complessa – data da Prisma a un gioco matematico, rivendicava l’importanza invece della geometria, usando la quale, nel medesimo gioco, la soluzione appariva decisamente più semplice. Partendo da questo spunto, la professoressa Dedò sottolineava quanto la geometria sia sempre più trascurata, per non dire ignorata, nell’insegnamento scolastico e le deleterie conseguenze che ciò comporta.

L’articolo ha riscontrato un sorprendente successo, con diverse centinaia di visualizzazioni in pochi giorni su www.prismamagazine.it e soprattutto ha cominciato a “rimbalzare” di forum in forum tra insegnanti appassionati di didattica della matematica e newsletters dedicate alla geometria, animando dibattiti profondi e davvero significativi e mostrando ancora una volta come il problema del ruolo sempre più minoritario della geometria nella scuola italiana sia molto sentito.

A titolo esemplificativo, riportiamo qui – con l’autorizzazione degli autori, ovviamente – alcuni di questi contributi (provenienti dalla pagina Facebook della Federazione Italiana Mathesis e poi passati sulla newslettter “MathNews”). Ci piacerebbe che il dibattito potesse continuare nelle sedi più diverse.

Gabriele Anzellotti

Anche a me, appena guardato il problema di Prisma, è venuto in mente di decomporre il quadrato in opportuni triangoli ed è stato evidente che l’area del quadrato era il doppio dell’area del trapezio. E concordo con Maria che, anche se si affronta il problema algebricamente, una volta vista la semplicità della soluzione dovrebbe venire da chiedersi se c’è una ragione geometrica semplice. Su questo stesso tema vorrei contribuire con una mia esperienza didattica all’università. Nell’insegnamento di analisi 1 a matematici, fisici e ingegneri mi è capitato in diverse annate di chiedere agli studenti di trovare l’area di un triangolo che avevo assegnato indicando le coordinate cartesiane dei vertici, ad esempio come nella figura qui sotto:

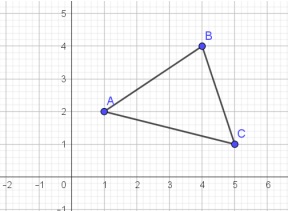
Questa mia domanda faceva parte di un percorso inteso a prendere consapevolezza della problematica della misura e dell’integrale. Il mio obiettivo era che gli studenti vedessero come si poteva ottenere l’area del triangolo ABC sottraendo all’area del rettangolo [1,5]x[1,4] le aree di tre triangoli, che si calcolano immediatamente come metà di certi rettangoli. La prima volta che ho fatto la domanda mi aspettavo che non sarebbe stata di risposta immediata da parte di tutti (anche se studenti di matematica e di fisica, che sono notevolmente autoselezionati). Ma si è rivelata più difficile del previsto e molti studenti si sono imbarcati a trovare un’altezza del triangolo, scrivendo l’equazione di un lato e della retta ortogonale, in modo da calcolare poi l’area come base per altezza diviso due. E questo è accaduto, come ho detto, con diverse coorti. Anche nel caso che ho descritto, come in quello indicato da Maria, è possibile che la strategia di decomposizione e sottrazione venga più naturale ai ragazzi e ragazze tra la fine della scuola media e l’inizio della superiore, come se gli studenti più grandi venissero in qualche modo ostacolati dalle conoscenze e procedure acquisite nella scuola superiore. Se qualche insegnante volesse fare qualche prova, sarei interessato a sapere cosa succede. Io non so se i fenomeni presentati indicano soltanto una “ignoranza della geometria”. A me sembra più in generale che nella scuola superiore, e anche all’università, l’insegnamento tenda a trascurare l’importanza dell’intuizione degli oggetti matematici e della capacità di “vedere”, e a ridurre la matematica, non solo la geometria, a manipolazione formale. Un esempio emblematico è il modo in cui si insegna l’algebra lineare al primo anno dei corsi di laurea, ma anche l’analisi matematica non scherza. Sulle ragioni di tutto questo io avrei qualche idea, ma non certezze, e il discorso sarebbe lungo e scivoloso, perciò mi fermo qui e ti ringrazio di nuovo.

Antonio Criscuolo

Le osservazioni di Maria Dedò sono preziose, e il suo esperimento didattico è dirimente. Per la formazione matematica dei nostri studenti, è essenziale privilegiare l’approccio geometrico-sintetico nella risoluzione dei problemi geometrici, piuttosto che quello geometrico-numerico/algebrico/analitico. Questo è particolarmente importante quando gli studenti iniziano a studiare l’algebra. Spostando l’attenzione dalle diverse possibili soluzioni alla formulazione del problema, si nota che esso contiene implicitamente l’indicazione: “risolvi questo problema applicando il calcolo algebrico”. Immagino che di fronte a quel testo molti studenti potrebbero fare queste osservazioni di questo tipo: c’è un numero (una misura), quindi ci devono essere delle formule (aree delle figure) e se le formule non bastano? Ci sono le equazioni, sono quelle che risolvono i problemi. Dai, cerchiamo di scrivere un’equazione… E la geometria si perde. Se avessi ancora delle classi a cui proporre problemi, adotterei due diverse formulazioni del problema: Risolvi il problema utilizzando l’algebra e la calcolatrice (punteggio massimo: 8). Risolvi il problema senza l’uso dell’algebra e della calcolatrice (punteggio massimo: 10). Se risolverai il problema in entrambi i modi potrai aspirare alla lode. Cosa ne verrebbe fuori? Quali i possibili riscontri?

Giorgio Bolondi

L’algebrizzazione pervasiva e intensiva del curricolo effettivo del biennio si estende anche al triennio, perché anche il calcolo differenziale spesso diventa solo il pretesto per continuare ad applicare le tecniche algebriche di manipolazione, necessarie per risolvere la maggior parte degli esercizi proposti dai testi e dagli esami. Vorrei però allora approfittare dello stimolo di Paolo per sottolineare che gli studenti del Liceo Scientifico- che effettivamente vivono sotto la spada di Damocle dell’Esame di Stato sono meno di un quarto degli studenti italiani. Per gli altri tre quarti possiamo muoverci più liberamente: troppo spesso ci capita di vedere la matematica nella scuola italiana da una prospettiva liceoscientificocentrica. Lo stesso, mi dicono, avviene ai colleghi di materie letterarie.

Maria Alessandra Mariotti

L’algebrizzazione pervasiva è legata alla facilità della ‘proceduralizzazione’, proceduralizzazione che le attività proposte nell’ambito dell’algebra favoriscono e sviluppano. La geometria sintetica non è facilmente proceduralizzabile, come chiaramente espresso da Paolino (nome di fantasia) di 5 primaria: “Per me la cosa più difficile della matematica sono i problemi di geometria perché non mi riesce capirli. Per me la matematica è un mondo di numeri. Secondo me la matematica è la materia più importante. A me la cosa che mi piace fare di matematica sono le divisioni a due cifre perché le ho imparate bene. Io non so fare i problemi perché non riesco a capirli”. Ho altri molti altri begli esempi di opinioni di allievi della primaria che riguardano la geometria … e le formule! La cosa che mi pare più interessante è che l’opinione di Paolino non è certo isolata; è per altro condivisa da molti insegnanti, e non solo certo della primaria. il declino della geometria si sta facendo strada, come qualche domanda indiscreta fatta ad insegnanti del Liceo (scientifico e non) mostra chiaramente a chi non si imbarazzi a porla. Le ragioni del declino della geometria sono molteplici e su queste si deve discutere per comprendere e magari per affrontare la paura della spada di Damocle!

Davide Germanò

Apprezzo soprattutto che ci siano ancora studenti capaci di formulare soluzioni alternative, mi fa ben sperare che qualcuno ancora riesca a salvarsi dal “piattume” intellettivo e intellettuale in cui incombe il nostro Paese. Cercavo di capire che cosa avrebbero risposto i miei studenti del Liceo di Assisi se avessi proposto loro questo quesito. Sono ragazzi del liceo delle scienze umane e del linguistico, dunque i loro curricula non prevedono grandi approfondimenti di natura scientifica. Tuttavia, a quanto pare, il quesito possono risolverlo anche allievi della scuola primaria, per cui immagino che, sebbene gli studenti delle scienze umane non si sentirebbero a proprio agio, teoricamente potrebbero saperlo risolvere. Ahimè dubito fortemente che qualcuno dei miei studenti lo sappia fare. Di sicuro non saprebbe risolverlo per via geometrica ma anche la via algebrica la vedo improbabile. Quali siano le cause del mancato sviluppo di queste competenze e abilità, in maniera semplicistica, si fa presto a dirle. È sufficiente considerare in che modo i ragazzi (ormai anche gli adulti) trascorrono il loro tempo. I social e il virtuale hanno la meglio. Senza voler demonizzare questi strumenti di informazione e comunicazione, rimane il fatto che, il modo con cui questi strumenti vengono vissuti può influenzare le nostre abitudini e le personali attitudini, togliendo la possibilità all’individuo di mettere in atto le proprie potenzialità. Si dice spesso che le nuove generazioni siano figli dell’estemporaneo. Ahimè la riflessione non è estemporanea se non per casi eccezionali. Dunque, tutto ciò che ha a che fare con le abilità riflessive si perde per dare spazio a procedure che per lo meno ci fanno ottenere, nella migliore delle ipotesi un risultato. Le generazioni attuali con il loro stile di vita non sono indirizzate verso la riflessione ma verso l’immediato. In matematica non c’è nulla che realmente sia immediato. Per alcuni abili nel mestiere di sicuro sì ma sappiamo bene che per arrivare a certe “rapidità” il percorso formativo ha richiesto sacrificio ma soprattutto tempo. Tempo che, a quanto pare, le nuove generazioni non possono (/vogliono/ne sono motivati) dedicare. Non mi stupisco allora del fatto che non si faccia più geometria. Nessun allievo dedicherebbe un’ora del suo tempo per pensare ad una costruzione geometrica e la relativa risoluzione di un problema propriamente detto. Il risultato sarebbe che si registrerebbero una marea di insufficienze che metterebbe in crisi l’azienda portata avanti dal dirigente scolastico (scusate il sarcasmo), oltre alla frustrazione professionale che già caratterizza buona parte delle nostre carriere. Io trovo menti sempre più lente … ragazzi che potrebbero fare moltissimo potenzialmente ma che scelgono, consciamente o inconsciamente, di vivere diversamente da come potrebbero o per lo meno vivere parte del loro potenziale. Quello, appunto, che gli consente estemporaneità. Quando noi eravamo ragazzi di scuola secondaria, dedicavamo molto tempo allo studio, non discutevamo le scelte didattiche del docente che a sua volta nemmeno lui poteva semplificare visto che doveva attenersi al programma ministeriale. Questi incastri non ci sono più e in una apparente libertà di insegnamento si contrappone un libertinaggio comportamentale fomentato da sistemi sociali e da scelte superficiali vocate all’estemporaneo. Il “tutto e subito” ha la meglio sul “qui e ora”. In quel “qui e ora” in cui l’intera consapevolezza dell’essere si esprime, si potenzia e arricchisce. La geometria dimenticata non perde terreno rispetto all’algebra, all’analisi o al calcolo delle probabilità. Dei settori della matematica, in maniera più evidente che negli altri, on geometria non si possono tirare fuori risultati immediati. Richiede grandi capacità riflessive al pari degli altri settori ma, questi ultimi, godono del vantaggio algebrico e analitico che consentono di ottenere qualche risultato apprezzabile rapidamente. Per concludere, non credo che sia una scelta didattica privilegiare il calcolo al pensiero geometrico o matematico in generale. Pare sia piuttosto un’esigenza sociale. Grazie per la vostra attenzione.

Antonella Moser

Buon pomeriggio, premetto che sono una nostalgica non solo dei problemi di geometria ma anche di quei intriganti problemi di trigonometria che ci occupavano la mente per almeno un anno intero durante il quarto scientifico, quindi apprezzo molto l’articolo della collega che pone l’attenzione sulla carenza odierna. In questo caso anche una mancanza di attenzione nel leggere il risultato. Aggiungo di mio che l’articolo potrebbe essere da spunto per sollevare un’altra questione sul problem posing&solving che ritengo importante. Nel proporre un problema, ci si aspetta che lo si risolva in un qualsiasi modo (e spesso è quello algebrico). Uno solo. È quello che propongono spesso le riviste, i testi scolastici. Una volta risolto (il risultato viene) si passa a risolvere il problema successivo (così si fa spesso in aula, così fanno gli studenti a casa). Proporre problemi con diverse strategie risolutive, impegnare tempo per confrontare queste strategie valutando un eventuale ottimizzazione dei procedimenti risolutivi (meno calcoli, meno risorse -mentali, temporali – impiegate, meno probabilità di errore) costituisce un approccio che potrebbe essere più funzionale a sviluppare competenze di problem solving. Specie quando le diverse strategie riguardano ambiti diversi, algebrico, grafico, geometrico. Potrebbe essere anche un modo bellissimo per far intuire agli studenti e alle studentesse che tutto torna in matematica, che questa meravigliosa disciplina offre vari modi, anche molto diversi fra loro, per verificare la correttezza di una strategia risolutiva, per risolvere un dubbio su una formula.

Mariangela Chimetto

vorrei riprendere il discorso sollevato dall’articolo di Maria Dedò segnalato da Luigi Tomasi, perché mi sembra che gli interventi nella lista, e in particolare quello di Gabriele Anzellotti e di Giorgio Bolondi offrano spunti di riflessione a vari livelli e sarebbe interessante se la discussione continuasse. Come suscitare, coltivare e mantenere negli anni l’attenzione agli aspetti geometrici e in generale l’intuizione in matematica? Come conciliare questa esigenza, specialmente alla secondaria, la necessità di acquisire e coltivare anche altri aspetti del pensiero matematico, come i metodi dell’algebra e dell’analisi, e soprattutto la necessità di fornire strumenti per l’esame di stato (e gli studi universitari)? Mi sembra che per quanto riguarda la secondaria alcuni suggerimenti siano già emersi dagli interventi di Antonio Criscuolo e Antonella Moser. Mantenere l’attenzione alla geometria, nell’accezione dell’articolo di Maria Dedò, parallelamente allo sviluppo di altri ambiti, è possibile. Un modo è per esempio quello di accettare, e anzi incentivare, l’uso di metodi diversi per la risoluzione di un problema. Certo, questo non è sempre facile, perché per poterlo proporre e gestire anche il docente deve coltivare in sè lo spirito geometrico. Immagino che questo non sia facile per gli insegnanti, e sono sempre di più, specialmente tra i giovani, che nel loro percorso di studi sono stati poco esposti alla geometria. Che fare? (Re)introdurre elementi di geometria nella formazione degli insegnanti? E quale geometria? Per inciso, sapere che un problema si può affrontare in tanti modi e che a volte la geometria offre il metodo più veloce e meno “calcoloso” può costituire un vantaggio anche nell’esame di stato, almeno nella mia esperienza. C’è però un altro problema, sollevato da Maria Alessandra Mariotti: spesso la geometria, fin da bambini, è percepita come difficile e rischia di essere rifiutata, meglio rifugiarsi in ambiti più “sicuri”. Probabilmente qualcosa del genere accade anche con ragazzi più grandi: quanta geometria si fa negli istituti professionali? Qui però secondo me bisognerebbe intendersi su quello che si intende per “fare geometria”. Intendiamo, come il Paolino della professoressa Mariotti, risolvere problemi, probabilmente con applicazione di formule su perimetro e area? Intendiamo dimostrare teoremi, alcuni dei quali ci sembrerebbero evidenti? Il fatto è, secondo me, che la risoluzione di problemi, così come la dimostrazione di teoremi, e forse anche il passo precedente, cioè l’argomentare, sono la punta di un iceberg che ha una base molto più ampia, che rischiamo di non “vedere”. Sempre Maria Dedò, per esempio nel libriccino “Alla ricerca della geometria perduta” elenca cinque “fili” per un percorso di geometria: osservare, misurare, classificare, rappresentare, argomentare. Quanti di questi fili ha potuto percorrere Paolino? Quanto ha manipolato, piegato, ritagliato, disegnato, lavorando da solo o in gruppo ? Quanto ha parlato delle sue esperienze sulle forme con i compagni e con l’insegnante? E quanto è stato abituato a osservare e riconoscere le forme nell’ambiente circostante? Per inciso, il discorso sui vari livelli ai quali si fa geometria vale anche per ragazzi più grandi: con ragazzi che, per vari motivi, non arrivano a dimostrare rigorosamente o a risolvere problemi complessi, dobbiamo proprio rinunciare a parlare, se pure in modo informale, dello spazio e delle figure? dobbiamo rinunciare a osservare, misurare, rappresentare, classificare? Si tratta di processi che a qualsiasi età e a livelli diversi possono permetterci di usare il pensiero geometrico per leggere, interpretare, modificare la realtà. Mi piacerebbe che di queste cose si continuasse a parlare.

Gabriele Anzellotti

Sono proprio d’accordo con tutto ciò che ha scritto Mariangela Chimetto e vorrei riprendere il suo discorso. Fra le molte cose che ha scritto scelgo di sottolineare un passo, che riporto integralmente qui sotto Qui però secondo me bisognerebbe intendersi su quello che si intende per “fare geometria”. Intendiamo, come il Paolino della professoressa Mariotti, risolvere problemi, probabilmente con applicazione di formule su perimetro e area? Intendiamo dimostrare teoremi, alcuni dei quali ci sembrerebbero evidenti? Il fatto è, secondo me, che la risoluzione di problemi, così come la dimostrazione di teoremi, e forse anche il passo precedente, cioè l’argomentare, sono la punta di un iceberg che ha una base molto più ampia, che rischiamo di non “vedere”. Sempre Maria Dedò, per esempio nel libriccino “Alla ricerca della geometria perduta” elenca cinque “fili” per un percorso di geometria: osservare, misurare, classificare, rappresentare, argomentare. Quanti di questi fili ha potuto percorrere Paolino? Quanto ha manipolato, piegato, ritagliato, disegnato, lavorando da solo o in gruppo? Quanto ha parlato delle sue esperienze sulle forme con i compagni e con l’insegnante? E quanto è stato abituato a osservare e riconoscere le forme nell’ambiente circostante? Sono convinto che i cinque verbi, i cinque “fili” di Maria Dedò, che Mariangela ha citato, siano di importanza fondamentale, e concordo con Mariangela che siano poco praticati nelle ore di matematica a scuola. E quando ci sono, spesso sono in contesti “anomali”, giochi, gare, laboratori, che sono quasi un’evasione, e dai quali si deve ritornare alla Matematica “vera” delle disequazioni o dello “studio di funzione” in occasione delle verifiche. Sono forse usate maggiormente in altre materie, Fisica, Disegno o materie tecniche, dove però temo che non vengano sviluppate adeguatamente le idee matematiche. Tanto meno i cinque fili si trovano negli insegnamenti di matematica all’università. E dunque allargo la domanda di Mariangela: quando il prof o la prof di matematica di Paolino ha potuto incontrarli nel suo percorso di formazione scientifica e culturale? Se gli/le è andata bene ha potuto fare qualcosa in qualche insegnamento dell’indirizzo didattico nella laurea magistrale, ma non è detto. Anche in questo caso vorrei portare un contributo a partire dalla mia esperienza didattica all’università. Negli ultimi dieci anni prima di andare in pensione ho insegnato Analisi matematica 2 agli ingegneri Civili e per l’Ambiente. In questo corso si dovrebbe imparare il linguaggio per parlare di forme, funzioni, curve, superfici in due e tre, e più, dimensioni; per capire il significato dei concetti, nonché le procedure del calcolo differenziale e integrale in più variabili, e quindi per fare gli esercizi, è necessario “vedere” un po’ gli oggetti e capire quali punti di vista sono migliori, in quale direzione conviene “affettare”, che parametrizzaione conviene adottare. Per questo non bastano tutti i software 3D del mondo — è necessario sviluppare una qualche capacità di intuire e visualizzare mentalmente le cose. A questo ho sempre dedicato molto tempo, cercando esempi e figure semplici ma significative, che costruivo sulla lavagna con i gessi colorati (oltre che con Geogebra, versione 5) in modo da mostrare anche i ragionamenti, le procedure e la tecnica di rappresentazione per realizzarli. Per molti anni, dalle interazioni con gli studenti e dagli elaborati scritti e dagli esami orali ho potuto concludere che non è stato un lavoro inutile. Non credo però che sia una cosa comune. Concludo, osservando che per sviluppare il calcolo differenziale in più variabili è necessario conoscere il comportamento delle trasformazioni lineari, e le rette, i piani e i sottospazi vettoriali, e saper descrivere e manipolare questi oggetti con gli strumenti dell’algebra lineare (vettori e matrici). In altre parole serve la geometria analitica. Ma dove si impara? In effetti, c’è un corso al primo anno di Algebra lineare e Geometria! peccato che in questo corso spesso non viene fatto neanche un disegno e non si capisce cosa c’entra il corso con la Geometria. Dunque nel mio insegnamento di Analisi 2, con calma, riprendevo le applicazioni lineari e le forme quadratiche in due e tre dimensioni e sviluppavo il linguaggio algebrico per parlarne, in modo che fosse chiara la visione geometrica dei segni e dei calcoli. Questo linguaggio ha innumerevoli usi nei modelli matematici e statistici, nella computazione scientifica e nell’intelligenza artificiale, ed è oggi forse la parte più importante dell’educazione matematica di base in tutti i corsi di laurea https://www.ams.org/notices/202205/rnoti-p813.pdf. Credo che si dovrebbe ragionare su come impararlo meglio, anche, nei dovuti modi, nei licei e tecnici (a cominciare dal primo anno), sostituendo buona parte delle cose che si studiano attualmente.