L’embolia del clima

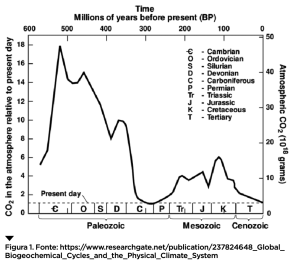
Un sommozzatore, quando torna in superficie dopo un’immersione, presta la massima attenzione, fa delle pause e consulta spesso il profondimetro e il cronometro. Ci si potrebbe chiedere il perché di queste accortezze: in fondo, se parte dal livello del mare, che cosa può succedere a un sub se torna allo stesso livello dopo l’immersione? Perché si preoccupa in questo modo? Perché una risalita affrettata potrebbe causare un’embolia e condurre alla paralisi o alla morte. Allo stesso modo, se questa domanda vi sembra ingenua, deve sembrarvi altrettanto ingenua la seguente: se nelle ere geologiche passate, tanto la temperatura quanto i livelli di CO2 sono stati anche più alti di oggi, allora, perché si parla tanto di “cambiamento climatico” e ci si preoccupa come se potesse derivarne una catastrofe per l’umanità? È una domanda maliziosa che si sente ripetere molto più spesso dell’analoga domanda sui sommozzatori e, a corredo di questo e altri slogan, si esibiscono dati assolutamente reali e corretti ma interpretati male o in modo parziale. Per esempio, guardiamo il grafico di figura 1 tratto da una pubblicazione scientifica. Se ne evince che la CO2 nell’atmosfera è oggi molto minore rispetto al Cretaceo, la fase finale dell’epoca dei dinosauri, quando era sei volte maggiore di oggi! Per centinaia di milioni di anni, il pianeta è stato più caldo e con concentrazioni di anidride carbonica ben maggiori dell’attuale. Ma allora hanno ragione i negazionisti del clima oppure, nel guardare questo grafico, stiamo trascurando qualcosa che ci sfugge? Consideriamo un sistema naturale, o anche economico o di qualsivoglia natura, che dipenda da un numero fissato di parametri che possono cambiare nel tempo (un parametro è null’altro che una grandezza misurabile). Per esempio, se ogni giorno alle 12 rileviamo la temperatura T in una certa località, il nostro sistema dipende da un solo parametro, cioè T. Se, invece, rileviamo la temperatura T, la pressione atmosferica P e la percentuale U di umidità nell’aria, il sistema è tridimensionale nel senso che ciascuna rilevazione dà luogo a una terna di numeri (T,P,U) e quindi a un punto nello spazio cartesiano a tre dimensioni. Questa tridimensionalità non riguarda lo spazio fisico ma solo lo spazio virtuale, lo spazio degli stati, le cui coordinate sono i parametri del sistema. La dinamica, ossia l’evoluzione nel tempo del sistema, è quindi descritta dal movimento del punto che in ciascun istante ne rappresenta lo stato, cioè da una curva nello spazio degli stati che si chiama traiettoria del sistema. Quel che accade in pratica è che spesso abbiamo a disposizione solo poche misurazioni, cioè non conosciamo la traiettoria se non per certi suoi specifici punti. Eppure, vogliamo spiegare il fenomeno, per cui ci occorrono le traiettorie passate, oppure dobbiamo prevederne gli sviluppi, per cui ci servono le traiettorie future. Come facciamo a determinarle anche solo in modo approssimato? Gli scienziati sanno, entro certi limiti di errore che si possono specificare, come rispondere a questa domanda: se abbiamo raccolto le misurazioni dei parametri di un sistema dinamico in certi ben precisi istanti, un opportuno modello matematico ci consentirà di tracciare traiettorie in accordo con i dati misurati proponendo valori possibili (e plausibili) laddove manchino le misurazioni. Esistono molti tipi di questi modelli ma qui concentriamoci su quelli deterministici introdotti a partire dal Seicento. Nella seconda metà del XVIII secolo Giuseppe Luigi Lagrange definì la dinamica di un sistema fissando per ogni istante una quantità, che oggi in suo onore chiamiamo lagrangiana, che fornisce il bilancio energetico del sistema stesso. La lagrangiana dipende non solo dallo stato del sistema al tempo ma anche dalla velocità con cui il sistema cambia in quel preciso istante (il tasso di variazione dei parametri, se vogliamo). Per esempio, se due particelle viaggiano lungo un segmento in direzioni opposte, l’una verso l’altra, prima o poi si scontreranno. Intuitivamente, se vanno a velocità molto basse, lo scontro sarà meno “violento” che se vanno a velocità alte, sebbene lo spazio percorso sia lo stesso in entrambi i casi. Infatti, la lagrangiana di questo sistema contiene un termine, l’energia cinetica, che cresce con il quadrato della velocità e determina la violenza dell’urto. Abbiamo già fatto l’esempio del sommozzatore che risale verticalmente e si sottopone quindi a uno sbalzo di pressione: il percorso che effettua nella risalita è esattamente quello che aveva effettuato nella discesa (quindi gli stati che assume nella risalita sono gli stessi che aveva assunto nella discesa) ma è la velocità con cui lo percorre che può causargli un’embolia anche fatale. Insomma, la velocità con cui cambiano gli stati di un sistema dinamico nel tempo è non meno importante degli stati che il sistema assume: senza di essa non è possibile studiare la dinamica del sistema. Per inciso, nella teoria quantistica il principio di indeterminazione di Heisenberg afferma proprio che non si può misurare con la precisione voluta tanto la posizione quanto la velocità di una particella. I sistemi quantistici sono quindi intrinsecamente non deterministici, sebbene una versione in dimensione infinita della teoria di Lagrange consenta di studiarli! Torniamo alla concentrazione di CO2 nell’atmosfera terrestre: dal 1870 a oggi, il suo valore medio è passato da 286 ppm (parti per milione) alle attuali 416 ppm, dunque con una velocità media di (416-286)/150=0,87 ppm/ anno, quindi in modo approssimato di 87 ppm/secolo. Poiché i carotaggi nei ghiacci antartici offrono dei dati che mostrano come negli ultimi 800.000 anni la concentrazione di CO2 abbia oscillato fra i 170 ppm e i 300 ppm e con una velocità media dell’ordine di 10 ppm/secolo, quella dell’ultimo secolo e mezzo è un’impennata clamorosa e inedita. Una sorta di “embolia del clima”, per rifarci all’esempio del sommozzatore.