La matematica dei ponti

Uno dei passatempi preferiti di noi matematici è “classificare”, ovvero suddividere un insieme di oggetti in classi a seconda di alcune loro caratteristiche. Per questo, c’è ponte e ponte. Se volessimo classificarli, prima di tutto effettueremmo una distinzione tra ponti fissi e ponti mobili e poi divideremmo quelli fissi in ponti a trave, capriata, continuo, a sbalzo, sospeso, ad arco o strallato e quelli mobili in smontabili, basculanti, girevoli, levatoi, sollevabili o a chiatta. In realtà, volendo essere proprio pignoli, sarebbe necessario cominciare facendo anche una distinzione legata al tipo di ostacolo che il ponte si trova a superare ma questa volta non saremo così raffinati e nel seguito useremo la parola ponte in modo indifferenziato, qualunque sia l’ostacolo attraversato.

I ponti ad arco

Come dice il nome, si definiscono “ad arco” i ponti in cui il piano viabile (su cui passano auto, treni, biciclette o pedoni) è sostenuto da una struttura ad arco, che può essere sottostante o sovrastante dando luogo a ponti ulteriormente classificati rispettivamente come “a via superiore” o “a via inferiore”. In architettura, l’arco si definisce come un elemento strutturale a forma curva che si appoggia su due piedritti (vedi figura 1).

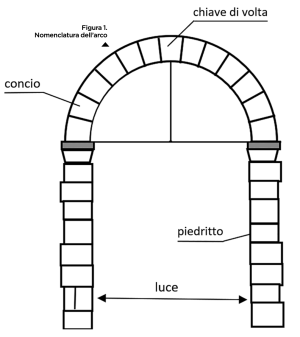
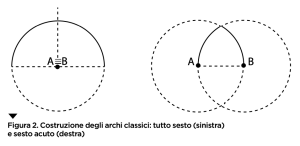
Gli archi che ci sono più familiari sono quelli a tutto sesto, ai quali ci ha abituato il sacro romano impero, e quelli a sesto acuto, tipici dei costruttori gotici. Tutti e due si ottengono contrapponendo due archi di circonferenza ma, nei primi, i due archi hanno lo stesso centro e lo stesso raggio, mentre in quelli a sesto acuto il raggio rimane lo stesso e il centro di ogni arco è situato alla base dell’altro (come mostrato nella figura 2).

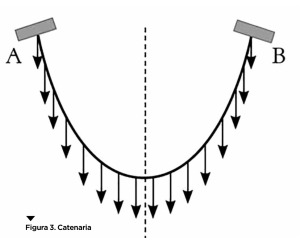
Dal punto di vista della distribuzione statica delle forze, un arco a tutto sesto è decisamente una struttura poco efficiente. Non potendo scaricare il suo peso in verticale (altrimenti cadrebbe), lo fa perpendicolarmente al piano di appoggio tramite i due conci che gli sono adiacenti. Così facendo, spinge i piedritti verso l’esterno. Quindi, se vogliamo che l’arco non crolli, dobbiamo ipotizzare una struttura decisamente massiccia per i piedritti e un contenimento laterale (detto contrafforte) che, contrastando la componente laterale della spinta, consenta loro di rimanere in piedi sostenendo anche il peso degli elementi che l’arco sorregge. Un po’ più efficiente è l’arco a sesto acuto, in quanto la risultante delle spinte dovute al suo peso e ai carichi sostenuti cade molto più vicino alla base del piedritto (ovvero ha una componente orizzontale minore). Si può fare a meno dei grossi spessori murari che fungevano da contrafforte nel caso dell’arco romano e si possono sostituire i massicci pilastri di sostegno con colonne più slanciate. “Stampelle”, le chiamava comunque con malcelato disprezzo Antoni Gaudí, l’architetto al quale piaceva un altro tipo di arco, che di stampelle può fare completamente a meno proprio grazie alla forma curva che si appoggia sui piedritti. Si tratta dell’arco catenario, struttura ottima nel senso (tecnico) che, a parità di materiale di costruzione, è quella di minimo peso in grado di sopportare un carico fissato. Lungo un arco catenario il carico è distribuito in modo omogeneo e per questo, a differenza degli altri due tipi di arco, questo sta in piedi senza bisogno di contrafforti o di altri elementi di supporto. Come lo si costruisce? Prendiamo una catenella o una corda e lasciamola pendere, tenendola per gli estremi, soggetta soltanto al suo peso. La curva che otteniamo si chiama catenaria e la sua forma assomiglia alla più comune parabola, ma ha un’equazione più complessa. Come indicato schematicamente in figura 3, la catenaria è soggetta solamente a forze di tensione: se quindi la ribaltiamo otteniamo un arco, l’arco catenario appunto, soggetto esclusivamente a forze di compressione.

Un tour italiano

Iniziamo il nostro percorso di osservazione di ponti ad arco da quello della Trinità di Firenze, originariamente opera di Bartolomeo Ammannati (pare su progetto di Michelangelo Buonarroti). Il ponte doveva la sua linea squisita, oltre che alle tre arcate di diversa ampiezza, ai peculiari piloni di sostegno e alle quattro statue allegoriche che ne decoravano gli angoli rappresentando le quattro stagioni. Dopo che fu distrutto nella notte tra il 3 e il 4 agosto 1944 dalle truppe tedesche in ritirata da Firenze, per poterlo ricostruire pari pari si pose in maniera pressante il problema di capire quale fosse la curva disegnata dai suoi tre archi. Nel giugno del 1952, il Comune di Firenze affidò l’elaborazione del progetto di ricostruzione all’ingegnere Emilio Brizzi e all’architetto Riccardo Gizdulich, rispettivamente per gli aspetti strutturali e per quelli formali. Grazie a un certosino lavoro dell’architetto, condotto a partire da fotografie storiche, il ponte fu ricostruito in tutta la sua leggerezza, dovuta proprio al fatto che i suoi archi sono catenari! Si basano sull’arco catenario anche diversi altri ponti nostrani, di costruzione molto più recente rispetto a quello fiorentino. Parliamo, per esempio, del ponte San Michele di Paderno, che può essere ammirato in tutta la sua imponenza percorrendo la pista ciclabile dell’Adda. È un ponte ad arco in ferro, a traffico misto ferroviario-stradale, che collega i paesi di Paderno e Calusco d’Adda attraversando una gola del fiume omonimo. Opera dell’ingegnere svizzero Jules Röthlisberger, è lungo 266 metri e alto 85, per una luce d’arco di 150 metri. Nel progettarlo, Röthlisberger applicò, una delle prime volte nella storia, i princìpi dell’ellisse di elasticità. Ne è risultato quello che è a oggi considerato un capolavoro di archeologia industriale, nonché una delle più notevoli strutture realizzate dall’ingegneria ottocentesca tout court. Passando al ventesimo secolo, uno dei ponti meglio documentati è quello sul Basento, in Basilicata, realizzato tra il 1971 e il 1976 dall’architetto Sergio Musmeci mettendo in pratica la sua teoria dei minimi strutturali. Un ponte imponente, che attraversa, oltre al fiume Basento, tre linee ferroviarie e due delle strade principali di Potenza. L’idea base della teoria di Musmeci è riassunta da questa sua frase: “Bisogna arrivare a delineare con una formula matematica una sola soluzione di natura statica per avere la certezza del migliore impiego, cioè il minimo peso, di una data struttura”. La particolarità della struttura di questo ponte è quella di essere costituita da una membrana unica di cemento armato con uno spessore uniforme di 30 cm, modellata a formare quattro arcate contigue. La lastra unica di cemento viene sia tirata e deformata, per creare delle specie di dita che sorreggono l’impalcato, sia ripiegata su sé stessa per creare un quadrato di 4 archi che sorreggono l’intero peso della struttura. Dal punto di vista matematico, questo ponte è molto interessante per almeno tre ragioni: la prima è il metodo di progettazione, in cui Musmeci combinò lo studio del comportamento di modelli fisici “concreti” con una serie di ingredienti squisitamente matematici, ovviamente applicati al problema ingegneristico-architettonico. La seconda riguarda i modelli che Musmeci era solito utilizzare: realizzati con vari materiali – tra cui pellicole liquide di soluzione saponata tese tra fili di cotone oppure semplici cordicelle con piccoli carichi – servivano a determinare strutture equitese che, rigirate, sarebbero diventate equicompresse. Lo studio delle pellicole saponate – le bolle! – ben lungi dall’essere un ingenuo gioco di ragazzini, costituisce non a caso un’importante branca della geometria differenziale. La terza ragione sta nell’osservazione che l’idea di un ponte realizzato tirando, deformando e ripiegando su sé stessa una lastra unica di cemento è profondamente topologica. Nella lista dei moderni ponti ad arco non può mancare quello di Bagnara, noto anche come Viadotto Sfalassà. Si tratta di un gigante con struttura mista in acciaio-calcestruzzo armato, progettato da Silvano Zorzi in collaborazione con Sabatino Procaccia e Luciano Lonardo e messo in funzione nel dicembre del 1972 come parte della Autostrada A3. Nella sua versione originaria era lungo 893 metri e presentava una campata centrale curvilinea con luce di circa 376 metri: enorme, impressionante. Tanto impressionante da essersi meritato per ben tre volte, durante la costruzione (rispettivamente nel 1968, 1970 e 1972), il Cecm European Award, massimo riconoscimento europeo per le grandi opere.

Ponti fissi creativi

Le “Vele di Calatrava” a Reggio Emilia e i “Ponti storti” di Bolzano sono due esempi di architettura topologica che ingolosiscono qualunque matematico. Con “Vele di Calatrava” si intende tutto il complesso architettonico progettato dall’archistar Santiago Calatrava, nell’ambito del progetto di riqualificazione della parte nord della città di Reggio Emilia: la stazione mediopadana dell’alta velocità, la copertura a onda del casello dell’autostrada A1 e appunto tre ponti imponenti di cemento armato e acciaio dipinto di bianco, visibili a chilometri di distanza. Quello centrale è un ponte ad arco a via inferiore, costituito da una luce di oltre 220 metri e con un arco centrale alto 50 metri circa, mentre i due ponti laterali sono entrambi strallati, cioè “sospesi”, retti da una serie di cavi (gli stralli) posti a disegnare un ramo d’iperbole. Con “Ponti storti” si intendono invece i due ponti che attraversano il fiume Talvera davanti al museo di arte moderna di Bolzano. Come il museo, anche i ponti sono opera dello studio berlinese KSV e, come per il museo, la matematica è cruciale nell’interpretazione della loro forma peculiare. Guardando i ponti con attenzione, notiamo che appaiono più “storti” dei ponti “normali”. Perché? È presto detto: se un ponte è perfettamente orizzontale, la sua linea centrale è dritta, cioè è un segmento di retta. Ci sono poi ponti, anch’essi orizzontali, un po’ più creativi, la cui linea mediana non è un segmento ma è una curva, che resta però sempre contenuta in un piano. La linea centrale dei due ponti del Museion, invece, è una curva con torsione per la quale, cioè, si può determinare un numero che misura quanto si allontana dall’essere piana. Curvatura e torsione sono proprietà che caratterizzano una curva nello spazio, misurando di quanto un tratto di curva si discosta dall’essere rettilineo (la curvatura) e di quanto si discosta dall’essere contenuto in un piano (la torsione). Tornando alle passerelle del Museion, ecco spiegato perché appaiono sensibilmente “storte”: la loro linea mediana è una curva con torsione diversa da zero e quindi la passerella stessa non è tutta contenuta su un piano ma è costretta a seguire la sua linea mediana nel suo percorso storto. Un bellissimo esempio di come la matematica ci possa aiutare a individuare e a descrivere con precisione che cos’è quel “qualcosa di strano” che a volte balza agli occhi e a cui, altrimenti, non riusciremmo a dare un nome.