Tentazioni simmetriche

Delizioso, non c’è altro attributo: pasta fritta fuori, dolce ricotta di pecora dentro e farcito in modo che la pasta rimanga friabile. Non c’è dubbio che il cannolo sia uno dei simboli della migliore sicilianità, assieme al carretto siciliano. Che sia in versione tradizionale o nell’adattamento fashion della collezione 2016 di Dolce e Gabbana o ancora nell’irresistibile versione motorizzata, il carretto è caratterizzato da un’esplosione di colori e … simmetria! In matematica una figura si dice simmetrica “se la possiamo dividere in due o più pezzi identici disposti in modo organizzato”. La simmetria cui siamo più abituati è quella bilaterale, che caratterizza volto e corpo umano e che condividiamo con molti altri animali: se prendiamo un viso, tracciamo una linea che lo divide in due verticalmente e appoggiamo uno specchio lungo tale linea, riusciamo a ricostruire il volto intero, segno che il nostro viso presenta appunto una simmetria bilaterale rispetto a quella linea verticale. Simmetria più o meno marcata a seconda dell’individuo, come possiamo vedere nella figura 1.

La simmetria bilaterale è però solo una delle possibili simmetrie che troviamo tanto in natura quanto nell’arte. Consideriamo, per esempio, u carrettu (il tipico carretto siciliano) della figura 2 e concentriamoci sulle decorazioni dei due scacchi interni dei masciddàra (le due sponde fisse del carretto), spesso riportate anche nel funnu di càscia (il pianale di carico del carretto) o sugli analoghi scacchi d’u puttèddu (il portello posteriore removibile).

Ne riportiamo lo schema in figura 3: da un centro di cui trascureremo la decorazione, si dipartono dodici “petali” bicolori, bianchi e blu in uno degli scacchi e bianchi e rossi nell’altro.

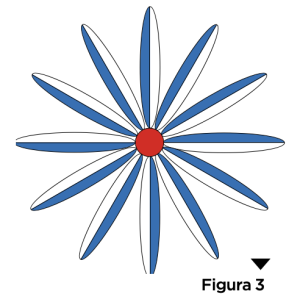
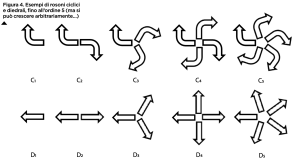
Chiamiamo quindi per semplicità “fiore” la decorazione complessiva. Se isoliamo uno dei petali e lo facciamo ruotare attorno al centro per dodici volte, possiamo ricostruire l’intero fiore. In altri termini, la rotazione di un dodicesimo di giro lascia invariata l’immagine del fiore, così come la riflessione rispetto alla verticale lascia invariata l’immagine del volto di Angelina: le due figure sono entrambe simmetriche, ma hanno una simmetria di tipo diverso. Nel primo caso parliamo di simmetria bilaterale, nel secondo di simmetria rotazionale. Le figure con simmetria rotazionale si chiamano rosoni. É lo stesso tipo di simmetria che ritroviamo nei rosoni delle facciate delle chiese. I rosoni che troviamo nelle decorazioni dei carretti siciliani, come quelli che ammiriamo sulle pareti delle cattedrali, non sono tutti uguali ma cambiano sia per quanto riguarda l’angolo della rotazione che li lascia invariati (ovvero l’ordine della rotazione), sia per qualcosa di più sostanziale. Alcuni, per esempio, sono conservati solo da rotazioni di angoli opportuni; altri, oltre alle rotazioni, ammettono anche riflessioni. I “fiori” del nostro carretto, per esempio, sono conservati solo da rotazioni ma, se trascuriamo la bicolorazione dei petali, allora ammettono anche riflessioni. E certamente ammettono sia riflessioni che rotazioni le ruote, anch’esse rosoni, che del carretto costituiscono naturalmente un elemento fondamentale! Forse vi stupirà, ma il primo a classificare tutti i possibili rosoni fu Leonardo da Vinci, che li divise in due grandi famiglie: ciclici (solo rotazioni) e diedrali (rotazioni e riflessioni). Sulle sponde del carretto ci sono però altre figure simmetriche, di natura diversa: si tratta dei fregi, tecnicamente definiti come “schemi piani periodici in una direzione”. Traducendo: un fregio consiste di copie ripetute, lungo una linea, di una singola figura o blocco (che chiameremo modulo). Nel fregio che orna la carrozzeria della Cinquecento siciliana, subito sotto il finestrino laterale posteriore, se non consideriamo il colore, il modulo è un semicerchio, che si ripete traslandosi nella direzione del fregio stesso.

Ma la traslazione non è l’unico modo in cui il modulo può ripetersi: se nel solito fregio della 500 consideriamo adesso il colore e “seguiamo” il percorso dei semicerchi azzurri, questi compaiono una volta con la concavità verso l’alto e la successiva verso il basso. Per ottenere la cornicetta, quindi, non sono sufficienti le traslazioni ma servono anche le riflessioni rispetto alla direzione del fregio.

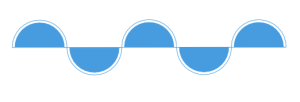
Viene quindi naturale chiedersi in quanti modi diversi è possibile, a partire da un modulo fissato, riempire una striscia di piano con un motivo periodico “basato” su quel modulo. Proviamo a stabilirlo a partire dal modulo del cannolo siciliano.

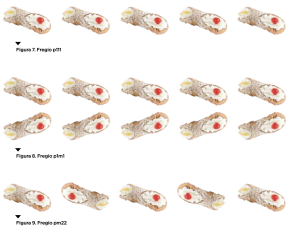
Il pasticcere poco fantasioso disporrà i suoi cannoli uno a fianco dell’altro (figura 7): a partire dal cannolo di sinistra, tutta la fila si ottiene per traslazione, esattamente come per il fregio della carrozzeria della Cinquecento. Lo chiamiamo fregio p111. Volendo però risparmiare un po’ di spazio, potrà pensare di disporre i cannoli in un modo un po’ più efficiente (figura 8): a partire dal cannolo in alto a sinistra, quello in basso a sinistra si ottiene per riflessione. La coppia di cannoli successiva si ottiene per traslazione: abbiamo un fregio che si definisce di tipo p1m1. Il pasticcere creativo vorrà forse distribuire i suoi cannoli secondo un fregio un po’ più originale (figura 9): sempre a partire dal cannolo di sinistra, il successivo ruota di 180° prima di traslare e così via per tutta la fila: si tratta di un saporito fregio pm22. La nostra intuizione ci dice che, a seconda della fantasia del pasticcere, le disposizioni periodiche che può trovare per i suoi cannoli sono tante, tantissime. Ebbene, neanche per sogno: se il pasticcere vuole conservare la periodicità dello schema in una sola dimensione, i modi possibili per disporre i cannoli sono solo 7! Compratevi una ventina di cannoli e cercate di individuare i 4 fregi mancanti: comunque vada, la scorpacciata finale varrà la fatica fatta.