Il fattoriale!

In matematica capita spesso di trovarsi a svolgere il prodotto dei primi n numeri naturali. I matematici hanno allora inventato un nome e un simbolo per tale operazione.

Chiamano fattoriale di n (indicato con la scrittura n!) il risultato della moltiplicazione dei primi n numeri naturali: n!=1·2·3·4·…·n. Ad esempio, si ha   6! = 6·5·4·3·2·1 = 720.

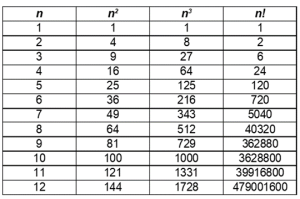
Si tratta di un operatore che porta molto velocemente ad avere numeri molto grandi, ancora più velocemente che con l’elevamento a potenza, come si vede nella tabella seguente:

Il fattoriale è di uso comune in matematica. Anche in alcune semplici situazioni che spesso si illustrano a scopo ricreativo.

Se n amici sono in posa uno fianco all’altro per una foto e il fotografo dice loro di disporsi a piacere, quante sono le possibili foto diverse che gli n amici potrebbero fare? In gergo tecnico, le possibili posizioni vengono chiamate permutazioni semplici e sono in numero di n!. Se gli amici sono 3, ad esempio Aldo, Baldo e Carlo, si possono disporre in 3! = 6 modi diversi: ABC, ACB, BAC, BCA, CAB, CBA.

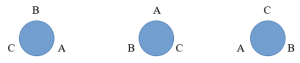
Se n amici sono seduti attorno a un tavolo (rettangolare, circolare, ellittico: non ha importanza la forma) e decidono di scambiarsi di posto, in quanti modo diversi possono mettersi? In gergo tecnico, le possibili posizioni vengono adesso chiamate permutazioni circolari e sono in numero di (n-1)!. Se gli amici sono 3, ad esempio, i già citati Aldo, Baldo e Carlo si possono disporre in (3-1)! = 2! = 2 modi diversi. Infatti, attorno a un tavolo, le permutazioni semplici ABC, BCA e CAB danno tavolate identiche tra loro

come pure BAC, ACB e CBA sono identiche tra loro se disposte in modo circolare