Nella letteratura poliziesca spesso i protagonisti delle indagini non sono poliziotti. A volte, sono addirittura dei religiosi come il don Matteo interpretato da Terence Hill, un prete di provincia che imbecca il brigadiere dei carabinieri con le sue intuizioni e che ha un antesignano nel padre Brown dei romanzi e racconti di Gilbert Keith Chesterton, portato sullo schermo da Renato Rascel nel celebre sceneggiato televisivo I racconti di padre Brown del 1970. Ma, come al solito, la realtà supera la fantasia. È esistito, infatti, un prete presbiteriano vissuto nel ’700 in Inghilterra le cui idee sono oggi utilizzate anche per risolvere dei casi giudiziari. Il reverendo Thomas Bayes aveva studiato logica e teologia a Edimburgo e aveva pubblicato un libro di matematica in cui difendeva la teoria newtoniana del calcolo differenziale dagli attacchi metafisici del filosofo Berkeley (anche lui un religioso). Aveva anche lasciato degli appunti, editi dopo la sua morte, dove si trova un teorema che è passato alla storia con il suo nome e che è alla base di una tecnica chiamata “inferenza bayesiana”, utilizzata in moltissimi campi, dalla finanza alla genetica, all’intelligenza artificiale e anche in ambito giudiziario e investigativo. Bayes fonda le sue idee sul concetto di “probabilità condizionata”. Supponiamo di essere sul finale di un’accesa partita del gioco dell’oca e che, lanciando entrambi i dadi, ci serva un 8 per giungere all’agognata casella finale. Per prima cosa, ricordiamo che lanciando un singolo dado la probabilità che esca uno dei sei possibili numeri è sempre la stessa: 1/6 = 0,1666… (le probabilità si esprimono solitamente con numeri fra 0 e 1 o in percentuali). Se invece lanciamo due dadi abbiamo 36 possibili esiti, che corrispondono alle coppie possibili di valori di ciascun singolo dado: (1,1), (1,2), (…), (6,5), (6,6). Il valore che ci interessa nel gioco dell’oca è la somma dei valori dei due dadi, una somma che va da 2 a 12. Ma queste somme non sono equiprobabili! Per esempio, la somma farà 2 in un solo caso su trentasei, quello che corrisponde a un 1 su entrambi i dadi (1+1), mentre la somma farà 3 in due casi su trentasei: 1 sul primo dado e 2 sul secondo oppure 2 sul primo dado e 1 sul secondo (1+2=2+1). La seguente tabella mostra tutte le combinazioni dei due dadi per fornire ciascun risultato possibile fra 2 e 12 e quindi la probabilità che una combinazione esca. La possibilità che esca 8 è 5/36 che corrisponde circa al 14%.
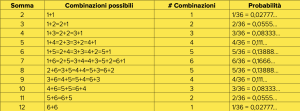
Per aumentare la suspense, supponiamo di lanciare i due dadi uno alla volta e che, lanciato il primo, esca 5. Al secondo lancio vorremmo che uscisse 3 in modo da avere 5+3=8. Poiché per un singolo dado tutti i numeri hanno la stessa probabilità pari a 1/6 di essere estratti, la probabilità che esca 3 al secondo lancio, e quindi che la somma faccia 8, è 1/6 cioè circa il 17%! Questo fatto si spiega osservando che nel secondo caso abbiamo un’informazione in più: al lancio del primo dado è uscito un 5. Dunque, l’unico risultato del lancio del secondo dado che ci potrebbe far totalizzare 8 è 3, che è equiprobabile agli altri. Quindi, la probabilità di totalizzare 8 con due dadi è il 14% ma la probabilità di totalizzare 8 con due dadi, sapendo che uno dei due fornisce 5, è il 17%. Oltre alla probabilità “a priori” P(E) che un evento E si verifichi senza tenere conto di alcuna informazione, abbiamo dunque anche la probabilità condizionata P(E|F) che E si verifichi sapendo che un altro evento F si è certamente verificato. Diciamo che P(E|F) è la probabilità di E dato F.
Nel nostro esempio: E=lanciando i due dadi la somma fa 8 e F=lanciando il primo dado esce 5. Quindi P(E)=5/36 mentre P(E|F)=1/6. Nessun paradosso. Stiamo soltanto calcolando probabilità distinte: una a priori, l’altra condizionata all’evento F. Notiamo che, se fosse G=lanciando il primo dado abbiamo 1, allora sarebbe P(E|G)=0! Infatti non è possibile ottenere 8 come somma di 1 con un altro numero fra 1 e 6 e un evento impossibile ha probabilità zero.
La nostra conoscenza di certi fatti legati a un evento cambia la sua probabilità di accadere! Le applicazioni al mondo dell’investigazione sono ovvie: se mia figlia sostiene di non aver mangiato l’ultimo budino al cioccolato nel frigorifero, dato che normalmente non mi dice bugie stimerò al 10% la probabilità che l’abbia fatto: innocente! Ma se attorno alla sua bocca ci sono evidenti tracce di cioccolato, la probabilità sale al 90%: colpevole! Se ho un indizio, non uso la probabilità “a priori” della marachella ma la probabilità condizionata alla presenza dell’indizio.
Un ben più tragico esempio è il caso dell’inglese Sally Clark, condannata nel 1999 per aver soffocato entrambi i figli: il giudice aveva stimato troppo improbabile che tutti e due fossero morti in culla, dato che la probabilità che un bimbo muoia di questa orribile sindrome era stimata 1 su 8.543 (lo 0,012%). Da ciò il giudice aveva dedotto che la probabilità di una doppia morte fosse il prodotto di queste due probabilità, cioè (1/8.543)× (1/8.543)=1/72.982.849 (poco più di un milionesimo per cento!) seguendo l’avviso del maggior pediatra, ma peggior probabilista, britannico che aveva scritto in un suo libro che “una morte in culla è una tragedia, due sono un sospetto, tre sono un omicidio, fino a prova contraria”. Nel 2001, la Royal Statistical Society screditò questa ipotesi (e il suo autore): la probabilità della morte in culla di un bambino è ben più alta se un suo fratello ha pure subito questa terribile sorte. Questa probabilità condizionata è più alta di un fattore che va da 5 a 10 rispetto a quella a priori. In presenza di informazioni su fatti certi, i giudici dovrebbero quindi usare la probabilità condizionata e non quella a priori. E infatti Sally Clark fu scagionata nel 2003, ma ormai la sua esistenza era stata rovinata e morì nel 2007 per intossicazione alcolica. Un altro esempio famoso è quello di O.J. Simpson, il campione di football americano messo sotto inchiesta per l’uccisione della ex-moglie e del compagno di lei nel 1994. Il processo che ne seguì è stato forse il caso giudiziario con maggiore copertura mediatica della storia, con la trasmissione in diretta sulle televisioni statunitensi delle scene della fuga in automobile dell’imputato. Un grave indizio a carico di Simpson fu il fatto che, quando erano ancora sposati, lui sottoponeva la moglie a maltrattamenti: la difesa tuttavia affermò che negli Stati Uniti le donne maltrattate erano circa 4 milioni ma che nel 1993, di queste, “solo” 1.432 erano poi state uccise. Un ragionamento agghiacciante per il solo fatto di considerare irrilevanti numeri così alti di femminicidio. In ogni caso, il verdetto del giudizio penale fu di innocenza. I difensori di Simpson avevano usato la cosiddetta “fallacia del procuratore”, in cui si confonde la probabilità della colpevolezza dell’accusato con la probabilità a priori del delitto. Nel caso di Simpson, la percentuale degli uomini che uccidono le mogli fra quanti le picchiano è irrilevante: l’informazione cruciale era che la moglie fosse stata effettivamente uccisa e quindi doveva essere considerata la probabilità che un uomo abbia ucciso la moglie nell’ipotesi che la picchiasse e che questa fosse stata assassinata. Con le nostre notazioni, la difesa aveva considerato la probabilità P(E|F) dove E=Una donna viene uccisa dal marito e F=Una donna è maltrattata dal marito, mentre la probabilità corretta da calcolare sarebbe stata P(E|F,G) dove G=La moglie è stata assassinata. Occorreva cioè stimare la probabilità di E dato il verificarsi tanto di F quanto di G. Qualcuno ha stimato nell’80% la probabilità che una donna trovata uccisa e in precedenza picchiata dal marito sia stata effettivamente uccisa da quest’ultimo. Alla fine, il processo Simpson fu riaperto in sede civile e l’imputato condannato a una pena detentiva, oltre che a un risarcimento milionario.
Ma che cosa c’entra il reverendo Bayes in tutto questo? Il fatto è che stimare la probabilità condizionata può non essere immediato e un modo di farlo fu suggerito proprio dal nostro stimato reverendo, che propose la formula P(E|F)=P(E,F)/P(F), dove con P(E,F) denotiamo la probabilità che E e F si verifichino entrambi, cioè la probabilità congiunta di E e F. Possiamo riscrivere questa formula come P(E,F)=P(F)×P(E|F). L’errore del giudice nel caso di Sally Clark è stato supporre che fosse P(E,F)=P(F)×P(E), il che è vero solo se E e F sono “indipendenti”, cioè se la probabilità di E non cambia a seconda che F si sia verificato o meno, in breve se P(E|F)=P(E). Notiamo che ovviamente P(E,F)=P(F,E) dato che la probabilità che E e F si verifichino è identica a quella che F ed E si verifichino! La definizione di Bayes consente quindi la catena di equazioni: P(F)×P(E|F)=P(E,F)=P(F,E)=P(E)× P(F|E) e il teorema di Bayes afferma precisamente che P(F×P(E|F)=P(E)×P(F|E). Il teorema ha una conseguenza sorprendente: se conosciamo le probabilità a priori sia di E sia di F, possiamo calcolare P(E|F) in termini di P(F|E) e viceversa! Infatti P(E|F)=P(E)×P(F|E)/P(F) e P(F|F)=P(F)×P(E|F)/P(E). Questo è importante perché, se E è la colpevolezza di un imputato e F un indizio a suo carico, quel che vogliamo calcolare è tipicamente P(E|F) mentre è più semplice stimare P(F|E). È più facile osservare quali indizi un criminale possa lasciare sulla scena del delitto piuttosto che calcolare quanto la presenza di questi indizi implichi l’effettiva colpevolezza di un indiziato. Un altro esempio è la diagnosi di una malattia E sulla base di un sintomo F: con un’enciclopedia medica potremmo stimare P(F|E) ma solitamente siamo interessati a P(E|F). Il teorema di Bayes, posto di saper stimare le probabilità a priori di E e F, ci consente di invertire la deduzione e calcolare P(E|F) in termini di P(F|E). Le applicazioni in campo forense potrebbero quindi essere non meno feconde di quanto non siano già state in campo medico. E riteniamo che la probabilità che il reverendo Bayes le avrebbe apprezzate, se le avesse potute conoscere, possa essere molto alta…
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
Una risposta
Espongo il mio caso in discussione presso il GdP. .Sono imputato peraver dato un calcio ad un ginocchio ad una condomina (segretaeia dell’assemblea) nel corso di un’assemblea condominiale, associato ad una frequente opposizione alle delibere condominiali in quasi tutte le assemblee effettuate da 40 anni. Applicando il teorema di Bayes (non si dispone di nessuna statistica di calci inferti né di percentuali di opposizioni alle delibere, se non di 490 assemblee, con in medi 3 delibere per ogni assemblea, dunque per un totale di 1470 opposizionii), sarebbe possibile calcolare la probabilità di aver inferto il calcio ??
Definisco le variabili come:
P(H/E)=probab. del dato il calcio; P(E/H)= prob .opposizione alle delibere = 240; P(H) = prob. condizionata = sconosciuta; P(E) = sconosciuta. Grazie.Grazie.