Tra miracoli e scacchi

Quel giorno chi li avesse visti giocare avrebbe subito capito, anche senza conoscerli, che si trattava di due grandi giocatori di scacchi: uno, il tedesco, era addirittura il campione del mondo in carica dal 1894 e l’altro, l’inglese approdato negli Stati Uniti nel 1887, era anche lui abituato a giocare ai massimi livelli. Ma se l’ipotetico spettatore avesse saputo solo questo, avrebbe perso un’informazione curiosa: erano tutti e due matematici e pure di valore. Al tedesco Emanuel Lasker va il merito di aver dato una mano a togliere l’algebra dal pantano in cui ormai affogava, piena di risultati che non sapeva ordinare e mettere a profitto. I suoi “ideali primari” permetteranno a Emmy Noether, la fondatrice dell’algebra del ventesimo secolo, di individuare quali proprietà dei numeri interi o dei polinomi si possono estendere ad altre situazioni magari meno maneggiabili, dando avvio a quella tendenza verso l’astrazione che insegna a pensare in termini semplici per raggiungere risultati del tutto generali.

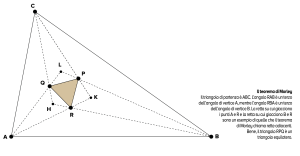
A Frank Morley, invece, professore di matematica alla Johns Hopkins University di Baltimora, la storia avrebbe attribuito addirittura un “miracolo”, quello di riuscire a generare da un qualsiasi triangolo un triangolo… molto regolare, addirittura equilatero.

L’affermazione di Morley è semplice e comprensibile da chiunque: “In un triangolo si dividano in tre parti uguali gli angoli interni. I tre punti di intersezione delle rette che realizzano la divisione e sono adiacenti fra di loro sono i vertici di un triangolo equilatero”.

Non si può trisecare un angolo solo con riga e compasso: questa è una delle impossibilità che hanno turbato di più i matematici (solamente all’inizio dell’Ottocento Évariste Galois è riuscito ad addomesticarla creando un campo del tutto nuovo di studi) ma per venirne a capo basta accettare di trisecare l’angolo con strumenti meno classici. Morley ricava la sua dimostrazione come caso particolare della situazione descritta in un altro suo teorema pubblicato nel 1900 ma la ricerca di una prova autonoma, condotta con strumenti della geometria elementare, durerà almeno fino al 1914 passando attraverso i tipi più classici del ragionamento matematico. C’è chi arriva al risultato per via diretta, un passo dopo l’altro a partire dal triangolo ABC e usando tutto l’armamentario tecnico a disposizione, compresa la trigonometria. C’è chi invece procede all’inverso. Parte da un triangolo equilatero e costruisce un nuovo triangolo di cui mostra che quello di partenza è il triangolo di Morley e che in questo modo non si ottengono soltanto triangoli “speciali” ma si può arrivare a un triangolo qualsiasi.

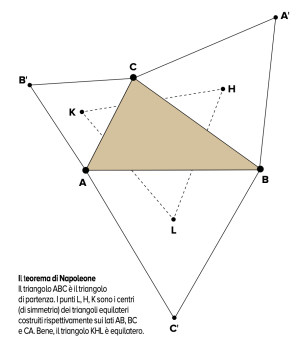
I triangoli sembrano più amichevoli di altre configurazioni e il miracolo di Morley non è il solo a gettare luce sulle regolarità che si possono associare anche al più sbilenco dei triangoli. Per esempio, di chi è l’affermazione: “Se sui lati di un triangolo costruite, fuori dal triangolo stesso, tre triangoli equilateri, allora i centri di questi nuovi triangoli sono i vertici di un triangolo equilatero”? Secondo molti, questo teorema è opera di Napoleone Bonaparte, cioè di un militare e statista che ha fatto della scienza (e della matematica) un pilastro della sua costruzione politica ma che non era certo un ricercatore. È stato W. Rutherford il primo a chiamarlo “teorema di Napoleone” nel 1825 sul- la storica rivista The Ladies Diary.

I rapporti dell’imperatore con i matematici del tempo erano figli sia della sua educazione all’Accade- mia militare – era sempre stato un allievo bravo in matematica e tutti sappiamo che, se hai provato il gusto della matematica almeno una volta da ragazzo, poi te lo porti dietro per sempre – sia dell’attenzione che, a partire dalla Rivoluzione, la Francia andava dedicando alla scienza e al contributo che gli scienziati potevano dare alla costruzione della nuova società. Ma i rapporti forti che stringe con matematici del valore di Monge, Fourier o Lagrange sono il frutto di una scelta solamente sua. Quanto a Monge, per esempio, lo nomina suo rappresentante quando si tratta di scegliere i testi antichi – fra i quali diverse opere scientifiche – che l’accordo con papa Pio Vi gli permette di rapinare in Italia. Poi se lo porta nella spedizione in Egitto insieme a un centinaio di altri scienziati grazie ai quali la spedizione – fallita dal punto di vista militare – diventa un successo di immagine destinato a durare nel tempo. Senza dimenticare che è alla scuola fondata da Monge, l’École Polytechnique, che affida l’alta formazione di quei tecnici – ingegneri militari – che permetteranno alla Francia di entrare da protagonista nell’Europa del XIX secolo e di restare a lungo la migliore potenza matematica al mondo. E all’École la matematica la fa da padrona!

E allora, anche se il teorema non fosse dell’imperatore, che importanza ha? Forse Napoleone l’aveva trovato in un testo del matematico bergamasco Lorenzo Mascheroni o forse ne aveva parlato con Lagrange che l’aveva dimostrato davvero. Lasciare il dubbio è anche un modo per ricordarci che la matematica è democratica: i teoremi non si preoccupano di chi li dimostra ma solo di essere veri! Comunque, se siete curiosi, sappiate che a vincere la partita a scacchi da cui siamo partiti per il nostro racconto è stato Morley, non il campione del mondo!