Esplorare la geometria piegando la carta

Capita abbastanza spesso che la matematica insegnata ai bambini e ai ragazzini più piccoli generi qualche mal di pancia e un senso di gravosa ineluttabilità: a differenza della gran parte delle discipline che incontrano a scuola, la scienza dei numeri e delle forme non ha grande attinenza con la loro vita. Tuttavia, bambini e ragazzi ammirano chi dimostra attitudine in ambito logico-matematico, amano enigmi e rompicapo e sanno cogliere le sfide intellettuali. Sta al loro docente solleticare questa attitudine sopita e lasciarla emergere affrontando esperienze, argomenti, temi in modo significativo procedendo, di pari passo con l’inevitabile ripetitività delle esercitazioni, con l’esplorazione della realtà e l’incontro/ scontro con i problemi.

L’Origami, la piegatura della carta, è un terreno di esplorazione in cui può essere molto interessante addentrarsi. Ormai molto conosciuto, diffuso e praticato come attività creativa per il tempo libero e in ambito scolastico, per lo più nella scuola primaria, l’Origami ha un’indiscussa valenza formativa come attività manuale. In esso però c’è molto di più di questo: ogni piega sulla carta ha un preciso significato geometrico.
La piegatura della carta integra l’uso degli strumenti da disegno. Piegando un foglio si possono costruire oggetti geometrici che, a differenza di quelli disegnati, possono essere manipolati e modificati e questo permette di riflettere sulle trasformazioni che l’oggetto subisce, dato che un certo tipo di piegatura può generare un ente geometrico piuttosto che un altro. La piegatura della carta è uno strumento per la comprensione della matematica che potrebbe accompagnare gli alunni per diversi anni.

A 9 o 10 anni (nella quarta e quinta classe della scuola primaria) i bambini hanno sviluppato delle capacità manuali sufficienti per intraprendere semplici percorsi di piegatura di carta. Esistono numerosissimi modelli semplici di origami tradizionali, non geometrici ma figurativi (la rana, la farfalla, la scatola…), che potrebbero essere piegati: un’attività che getta le basi per l’esplorazione geometrica. Nel piegare il foglio è richiesta la maggior precisione possibile; è un’attività che educa la coordinazione oculo-manuale e la manualità fine: portare un margine sull’altro, ripiegare una linea su sé stessa, operare sul foglio di carta con pieghe inusuali. Nel farlo, si costruiscono – ma con i più piccoli non è necessario precisarlo – assi di simmetria, bisettrici, perpendicolari.

Una delle pieghe che si incontrano più frequentemente, sia nella piegatura di modelli figurativi che nella costruzione di figure geometriche, è quella che sovrappone due margini consecutivi del foglio, portandoli uno sull’altro. Questa piega divide l’angolo compreso tra i due margini in due parti della stessa ampiezza.

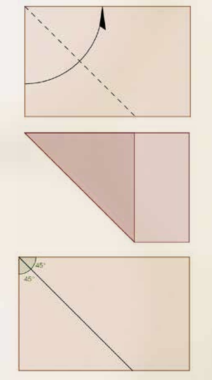
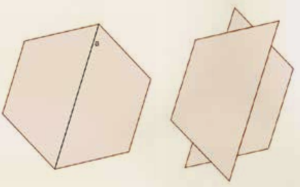
Il semplice gesto di piegare a metà un foglio di carta implica la costruzione di un asse di simmetria. Infatti nell’origami “piegare a metà” la figura significa mettere una parte del foglio sull’altra, facendo in modo che esse coincidano esattamente. In questo modo si ottengono due parti che possono essere sovrapposte l’una all’altra tramite la riflessione rispetto alla retta individuata dalla piegatura. Non bastano una traslazione e neppure una rotazione, cioè non bastano le isometrie dirette, come dicono i matematici. Occorre un’isometria inversa che spesso i ragazzi interpretano come il ribaltamento di una parte sull’altra, coinvolgendo così una trasformazione che esce dal piano del foglio e si avventura nello spazio.

Nella scuola secondaria di primo grado, gli alunni che nella scuola primaria hanno già familiarizzato con la piegatura possono iniziare un percorso un po’ più consapevole, ragionando su come alcune pieghe generino perpendicolarità, simmetrie o altro e utilizzando questa consapevolezza per costruire triangoli, quadrilateri particolari e poligoni regolari, analizzandone le proprietà ed esplorandone la simmetria. Gli approcci propedeutici compiuti alla scuola primaria sono fondamentali: la piegatura per la costruzione dei modelli geometrici richiede una certa perizia ed è importante che l’impegno manuale non assorba tutte le energie, che non travalichi l’esplorazione geometrica, principale scopo di tutta l’esperienza.

Nell’ultima classe della scuola secondaria di primo grado e, successivamente, nella scuola secondaria di secondo grado, padroneggiate ormai le abilità manuali necessarie, la costruzione di modelli anche più complessi spianerà la strada alle dimostrazioni e alla realizzazione di solidi geometrici. Costruire un origami significa imparare a seguire indicazioni operative che richiedono attenzione, concentrazione, comprensione piena, per esempio di espressioni come “sovrapponi il margine destro del foglio e il margine sinistro”, oppure “ruota il foglio”. Seguire istruzioni impartite a voce, imparare a decodificare una specifica simbologia e acquisire un lessico specifico sono tutte competenze

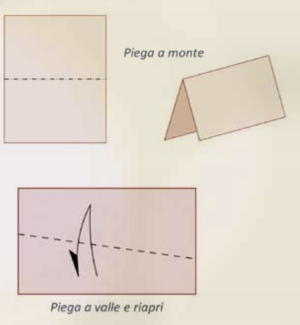
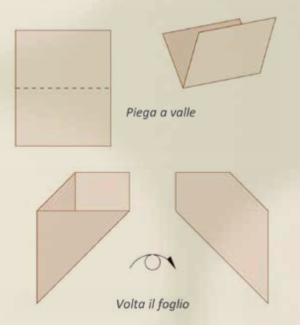
che sono richieste anche nell’apprendimento della matematica. E non è una questione da sottovalutare. A volte stupisce constatare come indicazioni che a noi adulti sembrano semplici, per bambino o un preadolescente non siano affatto scontate. Abbiamo dimenticato come eravamo a 12 anni! Quando, alle prime battute, diciamo: “Portate un margine del foglio sull’altro”, i ragazzi rimangono disorientati e chiedono spiegazioni ulteriori. Quando diciamo: “In un triangolo rettangolo, l’area del quadrato costruito sull’ipotenusa è uguale alla somma delle aree dei quadrati costruiti sui cateti”, non è che gran parte di loro affermerebbe di aver capito solo per farci contenti? Una volta o l’altra dovremo aprire un dibattito approfondito sul valore delle definizioni e degli enunciati nella scuola del primo ciclo!

Se vogliamo guidare gli alunni nell’esplorazione, dobbiamo imparare a conoscere chi abbiamo davanti e a comprenderne il modo di pensare; perché ciò accada, per trovare la chiave, dobbiamo lasciarli fare, agire, raccontare. Occorre tempo, certo, ma il guadagno sarà enorme. Quel tempo sarà stato speso in modo molto più proficuo che enunciando formule da memorizzare.

Ad esempio, tornando alle piegature, se chiediamo agli studenti di piegare un foglio, essi sovrappongono due metà per farle combaciare, senza pensarci due volte. Se però chiediamo di piegare il foglio senza sovrapporne i margini, dimostrano una certa riluttanza e difficoltà. State pur sicuri che, quando vedranno la piega ottenuta, qualcuno immancabilmente dirà: “È storta!”. Questo “incidente” fornisce interessanti spunti di riflessione. Dimostra infatti che i ragazzi prendono inconsapevolmente come riferimento i margini del foglio, oppure la quadrettatura. Ma noi ne approfitteremo per accendere il dibattito sulla linea “storta”. Perché è storta? Che cosa si intende per “storta”? Come dovrebbe essere la linea per poterla definire “dritta”?

Incappare in inconvenienti, lasciare questioni aperte, discutere… tutto ciò rende la lezione più interessante, permette a ciascuno di formulare la propria ipotesi e trasforma una trasmissione unidirezionale di informazioni in un confronto. Naturalmente, come docenti dobbiamo tenere le fila della discussione e la barra del timone, sapendo dove vogliamo portare i ragazzi, ma questa è un’altra storia.