TOPOLOGIA: Le forme dell’inconscio

Utilizzare la matematica per spiegare la psicanalisi, approfondire alcuni movimenti psichici a partire da movimenti analoghi di figure nello spazio, parlare di filosofia utilizzando forme geometriche: tutto ciò è possibile. Così come appassionarsi alla topologia anche se si ha una formazione filosofica e si vive tra libri come Così parlò Zarathustra di Nietzsche oppure Essere e Tempo di Heidegger.

La topologia è un settore della matematica che studia gli spazi e le figure geometriche in base alla loro forma (al termine forma diamo qui un senso così largo che in realtà le figure studiate possono essere deformate quanto si vuole purché non subiscano rotture o strappi). Ha un forte potere comunicativo e un grande fascino: abbatte subito tutte le barriere che qualsiasi neofita potrebbe avere nei suoi confronti, conquistandolo irrimediabilmente. Non utilizza numeri: potreste non vederne nemmeno uno, sul quaderno di un topologo. Oggetto di indagine sono le relazioni tra i vari punti di uno spazio e le forme che essi creano, indipendentemente dalle loro misure. Parla per immagini quindi, immagini in movimento.

Prendete un rettangolo, che possiamo immaginare come il piano di gioco di Snake. Il serpente esce dallo schermo del nostro Nokia 3330, poi rientra per uscire nuovamente di lato. Ma su che figura geometrica si sta muovendo, secondo voi? Provate a immaginare di piegare il rettangolo in modo da farlo diventare un cilindro, con i lati corti leggermente smussati. Ecco, questa è la base di Snake. Se uniamo poi le due circonferenze di base del cilindro, otteniamo un toro, una figura topologica che assomiglia a una ciambella.

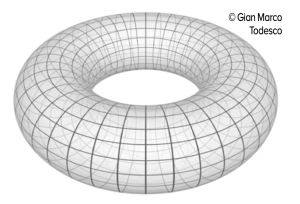
Unendo invece la superfice interna di un lato con quella esterna dell’altro, otteniamo una bottiglia di Klein. E qui, la mia mente inizia a viaggiare. Si tratta di una figura difficilmente pensabile e ancora più difficilmente rappresentabile. In uno spazio a tre dimensioni (3d) è impossibile ottenerne un modello che non abbia autointersezioni e quindi è impossibile “vederla”. Aggiungendo una dimensione, la questione diventa più semplice ma resta comunque complessa.

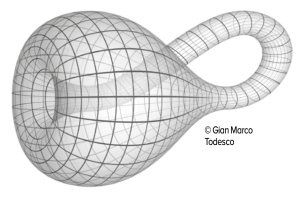
Ci sono molte figure in topologia che non si possono rappresentare come sottoinsiemi dello spazio ordinario a tre dimensioni ma che possono essere “immerse”– questo è il termine tecnico – in spazi con un numero di dimensioni superiore a 3.
Un altro esempio è rappresentato dalla figura degli anelli borromei: tre anelli interconnessi in modo tale che la scissione di uno provoca la separazione degli altri due. Si tratta di un oggetto immergibile in uno spazio 3d ma non in un piano; quindi, rappresentando gli anelli con carta e penna su un foglio, è davvero difficile percepire la loro proprietà principale, che poi è il motivo che lo rese il simbolo araldico dell’alleanza fra la famiglia Borromea e le famiglie dei Visconti e degli Sforza. Ma in tre dimensioni il legame tra gli anelli diventa evidente.

Qui si apre il paradosso: la bottiglia di Klein e tutte queste figure esistono o no? Il fatto che sia impossibile rappresentarle in date condizioni non nega forse loro il carattere ontologico dell’esistenza? Ma gli oggetti che possono solo essere pensati esistono oppure no? A ben pensarci, è un po’ come chiedersi se esistano le idee platoniche, modelli pensabili e perfetti di oggetti reali. Prima di tutto, per rispondere, bisognerebbe mettersi d’accordo su cosa vuol dire esistenza, e la filosofia non c’è ancora riuscita. Però, forse proprio il paradosso insito in queste figure apre uno spazio di pensiero che è tutto loro, e in fondo è reale. Tale spazio sta a cavallo tra l’esistenza e la non-esistenza, rappresenta il confine tra ciò che è pensabile e ciò che è rappresentabile. Proprio in questo luogo avvengono le trasformazioni delle figure topologiche, avviene la matematica, avvengono le idee.

A ben guardare, anche noi umani siamo frutto di un paradosso, esseri di confine. Da Freud in poi l’uomo è visto come diviso tra una parte più superficiale e l’inconscio, nascosto ma capace di condizionare il nostro agire quotidiano. Sarebbe tutto più semplice se la smettessimo di considerare la nostra vita inconscia come qualcosa che si svolge “sotto”. Anche perché così sembra facile nasconderla, ignorarla. Salvo poi svegliarsi un giorno e capire di non aver compreso noi stessi. Pensiamo alla struttura dell’analisi psicanalitica, che prende in considerazione l’avvenire di comportamenti talvolta patologici, che da Freud in poi possono essere chiamati sintomi, per collocarli nella storia della vita psichica del soggetto e comprenderne così l’origine.

Il linguaggio con il quale l’inconscio parla allo psicanalista è tutt’altro che logico e, per comprendere come funziona, inaspettatamente può venire in nostro aiuto la topologia. Una figura topologica è, e allo stesso tempo non è, autoevidente. Come dice F. Morales Montier in L’uso della topologia nell’analisi psicanalitica, la presentazione più comune di un toro “non è l’unica possibile: esso infatti, può essere deformato fino a raggiungere una tazza con il manico bucato: in questo modo, la superficie di una ciambella e la superficie di una tazza risultano topologicamente indistinguibili. Da un certo punto di vista, è ovvio che queste figure siano diverse. Tuttavia, in topologia sono uguali“.

Siamo sempre abituati a lavorare e pensare con oggetti che significano esattamente quello che sembrano. Non possono essere messi in discussione, ma solo misurati. I pensieri, i comportamenti, i neurotrasmettitori: li analizziamo come se non cambiassero nel tempo, ci fidiamo delle loro basi solide. Complice di questa credenza è la geometria euclidea, che prende i punti per quello che sono e ammette i movimenti purché le distanze rimangano inalterate. Ma, ed è un grande ma, come sostiene ancora Morales Montier: “Non tutto, nell’esperienza umana, si significa da sé. La psicoanalisi funziona con i significanti: elementi che non significano da sé. L’operazione analitica punta a stabilire che il detto non è identico a se stesso, e in questo modo può produrre e rivelare significanti. La psicanalisi è un dispositivo di de-materializzazione o, piuttosto, di ricollocazione della sostanza al proprio posto, in quanto deduzione”.

Ecco perché la topologia è stata spesso utilizzata in psicanalisi. Grazie ad essa, è più facile rappresentare alcuni fenomeni psichici, dar loro un volto per non lasciarli “sotto il tappeto” della superficie, la nostra vita conscia. Un esempio? Pensiamo alla realtà psichica come se fosse un movimento circolare che si sviluppa su un toro, la simil ciambella di cui parlavamo prima, attorno al vuoto centrale che sta per i nostri desideri, le nostre paure più profonde, le esperienze che abbiamo vissuto e poi rimosso. A questo punto, proviamo a compiere un’operazione: apriamo il nostro toro e torniamo al cilindro e quindi al rettangolo da cui eravamo partiti. Procuriamo una torsione a quest’ultimo prima di unirne due lati: ecco il nastro di Moebius, una struttura che, come la bottiglia di Klein, ha solo una faccia, una sola superficie.

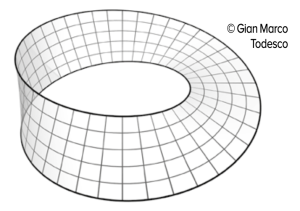
Paradossale come la bottiglia, amato dal pittore Escher che l’ha rappresentato in molte versioni, unisce il sotto e il sopra, il dentro e il fuori, ciò che si nasconde e ciò che appare. Ogni nostra azione, parola, manifestazione, è frutto della dialettica tra conscio e inconscio. Dialettica che però gioca su una sola superficie, l’unica possibile: noi stessi, il nostro corpo, il nostro essere nel mondo.