Il valore doppio di un teorema

La parola dualità è molto usata in matematica, anche se la sua introduzione è relativamente recente. La si deve al matematico francese Joseph Diez Gergonne (1771-1849). Inizialmente, Gergonne aveva scelto la carriera militare. Si arruolò con il grado di capitano nell’esercito di una Francia appena uscita dalla rivoluzione e partecipò nel 1792 alla battaglia di Valmy che insegnò ai francesi che le potenze contro-rivoluzionarie di Austria e Prussia potevano effettivamente essere sconfitte.

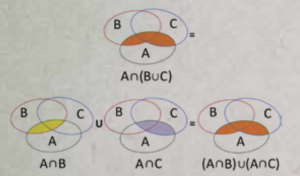
Trasferito a Nîmes con il suo reggimento, Gergonne trovò un posto da professore di matematica, lasciò l’uniforme e da quel momento si dedicò all’insegnamento e alla ricerca. Nel 1826, in uno dei suoi scritti, osservò che nella geometria che stava studiando, nel piano, a ciascun teorema ne corrispondeva un altro che si otteneva semplicemente scambiando fra loro le parole punto e retta (punto e piano, se fossimo nello spazio). Parlò di “cette sorte de dualité des théorèmes”. Et voilà, il termine dualità faceva il suo esordio in campo matematico. Da allora viene usato per designare, in generale, una situazione in cui due elementi o due figure o due spazi giocano un ruolo simmetrico, speculare, e possono essere tranquillamente scambiati fra loro dando luogo a affermazioni ugualmente vere (a patto che lo fossero quelle originarie). L’esempio più semplice viene forse dalla teoria degli insiemi. Le due proprietà distributive (di unione e intersezione) sono duali perché si passa dall’una all’altra scambiando tra di loro i simboli di unione e di intersezione.

Siccome i connettivi logici “e” (congiunzione di due affermazioni) e “o” (disgiunzione non esclusiva) corrispondono rispettivamente all’intersezione e all’unione della teoria degli insiemi, si capisce subito come la dualità trovi un campo fertile per le sue applicazioni anche nella logica delle proposizioni. Ma lo stesso succede nell’analisi matematica o nella teoria dei grafi o in altri ambiti. La geometria proiettiva, in un certo senso la geometria che nel piano dà cittadinanza anche ai punti all’infinito delle rette e non si occupa delle questioni di misura, rimane però il settore in cui il concetto di dualità trova probabilmente la sua migliore realizzazione. Dobbiamo la costruzione sistematica di questa geometria a un altro matematico francese, anche lui soldato ma questa volta dell’esercito napoleonico, Jean Victor Poncelet (1788-1867). Fatto prigioniero durante la campagna di Russia nel 1812, poté rientrare in Francia solo dopo due anni. Li trascorse a cercare di ricostruire la geometria che aveva studiato nei suoi studi da ingegnere e a prepararne quella presentazione che sarebbe stata una delle basi della crescita tumultuosa della ricerca geometrica nell’Ottocento. Il principio di dualità vi appare come uno degli elementi che gli permettono di mettere ordine nella massa di risultati eterogenei che costituivano il corpus geometrico a sua disposizione e nasce da un’osservazione che, come spesso accade, a posteriori sembra elementare. Alla base della geometria proiettiva sul piano stanno due affermazioni: “per due punti passa una e una sola retta”, la prima, e “due rette si incontrano in uno e un sol punto (se le rette sono parallele il punto sarà all’infinito e individuerà la loro comune direzione)” la seconda. Sono due affermazioni che si scambiano l’una con l’altra pur di sostituire alla parola “punto” la parola “retta”, al verbo “passare” il verbo “incontrarsi” come se fossero due diverse apparenze dallo stesso verbo “appartenere”. Due punti appartengono ad una e una sola retta diventa: due rette appartengono a uno e un solo punto. Dove sta il valore di questo principio? Anzitutto, nella grande economia di pensiero che consente solo punti, rette e questioni di appartenenza, con le sostituzioni indicate se ne ricava un’altra altrettanto “vera”. Teoremi che coinvolgono un triangolo e i suoi vertici possono diventare teoremi che coinvolgono un triangolo e i suoi lati; teoremi che coinvolgono una conica e i suoi punti si trasformano in teoremi che coinvolgono una conica e le sue rette tangenti. Possiamo scegliere quello che ci piace di più e ricordare solo quello. Un bel risparmio, anche di carta! Ma non è tutto qui. A volte, un fatto geometrico interpretato in termini di punti appare molto complicato, poco evidente, mentre la sua traduzione per dualità non solo è molto più semplice da dimostrare ma ci lascia intravvedere sviluppi che non avevamo immaginato. E questa è una buona cosa.

Dopo queste origini nella geometria proiettiva, una teoria della dualità si è sviluppata in molti altri settori della matematica. Già ne citavamo alcuni. Un altro è rappresentato dall’ottimizzazione, che consiste nella ricerca dei punti di massimo o di minimo di una funzione obiettivo (e nella ricerca dei valori che questa associa a tali punti). In un problema di ottimizzazione, la funzione obiettivo è spesso accompagnata da una funzione di vincolo, quando siamo vincolati a determinate condizioni e non siamo liberi di attribuire qualsiasi valore alle variabili. Si parla allora di problemi di ottimizzazione vincolata.

Ad esempio, quando un consumatore va a fare la spesa, il suo obiettivo è massimizzare la propria utilità (ovvero il piacere di avere determinate merci) ma non è libero di spendere qualsiasi cifra; è vincolato dai 100 euro, ad esempio, che ha nel portafogli. Non può scegliere qualsiasi paniere di beni – altrimenti la scelta sarebbe quella di riempire il carrello all’inverosimile – ma deve limitarsi a scegliere il paniere che gli dà la massima soddisfazione tra quelli che costano complessivamente 100 euro (o rimangono entro questa cifra). Ebbene, in ottimizzazione, nella teoria della dualità, a un problema di questo tipo se ne associa un altro – detto appunto duale – che presenta magari minori difficoltà computazionali e risulta più semplice da risolvere. Naturalmente deve sussistere una qualche relazione tra le soluzioni del problema originario e quelle del suo duale.

Ci sono vari modi di formulare il duale di un problema di ottimo. In ogni modo, se il problema originario è di massimo (cercare punti e valori di massimo), il suo duale sarà di minimo, e viceversa. La funzione obiettivo del problema originario diventerà il vincolo in quello duale e la sua funzione obiettivo sarà costruita attraverso il vincolo del problema iniziale; in altre parole e sbrigativamente, nel passaggio dal problema originario al duale, funzione obiettivo e funzione di vincolo diventano speculari e si scambiano di ruolo.

Come esempio, supponiamo di voler trovare il rettangolo che ha l’area massima (l’area è la funzione obiettivo) tra tutti quelli che hanno un certo perimetro (il vincolo sia, ad esempio, che il perimetro sia di 16 cm). Passiamo al suo duale, scambiando max con min e funzione obiettivo con vincolo. Con questa costruzione del duale, si parla in particolare di problema reciproco. Imposteremo allora la ricerca del rettangolo che ha il perimetro minimo tra tutti quelli che hanno un’area di 16 cm². In questo caso, i due problemi sono addirittura equivalenti e danno la stessa risposta: il rettangolo cercato è il quadrato di lato 4 cm. È come dire: il prodotto di due numeri positivi di somma costante è massimo quando i due numeri sono uguali oppure la somma di due numeri positivi di prodotto costante è minima quando i due numeri sono uguali. L’insieme delle soluzioni del problema originario coincide con quello delle soluzioni del problema duale, come accade in ogni problema di ottimizzazione vincolata sufficientemente regolare, in cui le funzioni coinvolte soddisfano determinate proprietà.