La sinfonia cosmica delle stringhe

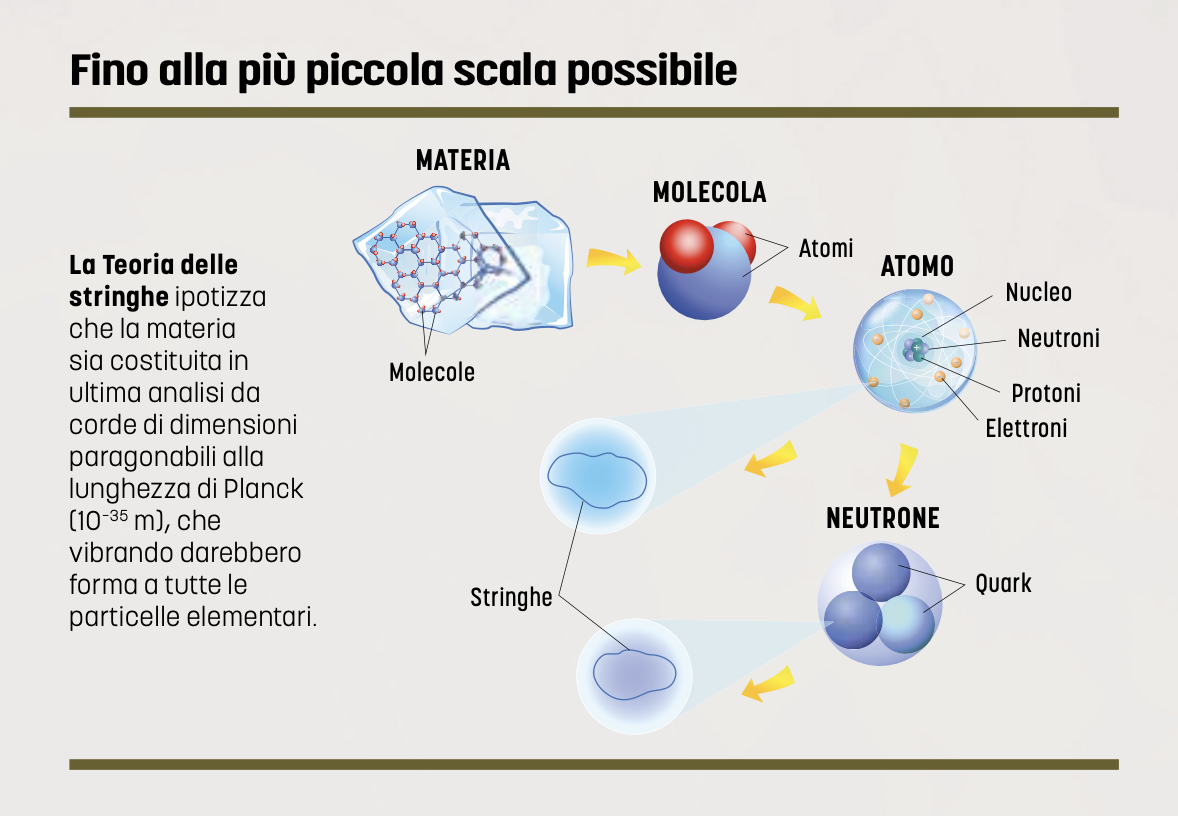
Un concerto per archi in un universo a dieci dimensioni. Una sinfonia di piccolissime cordicelle vibranti che genera la materia, le forze fondamentali e tutta la fisica che conosciamo. Secondo la Teoria delle stringhe, una fra le idee più ambiziose e affascinanti della fisica dell’ultimo secolo, l’universo non sarebbe costituito di particelle puntiformi, ma di stringhe, cordicelle vibranti piccolissime, dell’ordine della “lunghezza di Planck”: un milionesimo di miliardesimo di miliardesimo di miliardesimo di centimetro (o 10^-35 m). Come le corde di un violino producono suoni diversi secondo il modo in cui vibrano, così le diverse oscillazioni delle stringhe darebbero luogo a tutti i fenomeni che osserviamo.

Una “Teoria del tutto”

La Teoria delle stringhe è un tentativo di arrivare alla cosiddetta Teoria del tutto conciliando le due idee che hanno rivoluzionato la fisica del Novecento: Relatività generale e Meccanica quantistica. La Relatività generale descrive il mondo macroscopico e tutti i fenomeni gravitazionali. A grandi scale la gravità è la forza dominante, determina il nostro peso, il comportamento dei pianeti, la forma e la struttura delle galassie e dell’intero universo. La Relatività generale lega questa forza alla geometria – o meglio alla curvatura – dello spazio-tempo, che è determinata dall’energia e dalla materia in esso contenute. Il comportamento della materia su scala subatomica è invece governato dalla Meccanica quantistica, che descrive le altre forze fondamentali (elettromagnetica, nucleare forte e nucleare debole) e le particelle come gli elettroni o i quark. Se la Relatività è geometria, la Meccanica quantistica è probabilità: tutti i processi che descrivono le interazioni tra particelle sono di tipo probabilistico. Le due teorie funzionano bene alle rispettive scale, ma danno problemi se si cerca di considerarle contemporaneamente, perché introducendo la Relatività nel modello quantistico i calcoli portano spesso a valori infiniti. E gli infiniti suonano per i fisici come un campanello d’allarme: per avere significato fisico, le grandezze devono assumere valori finiti. Relatività e Meccanica quantistica d’altronde non possono essere tenute separate, perché esistono luoghi dove estremamente grande ed estremamente piccolo convivono. Per descrivere il nostro universo subito dopo il Big Bang, oppure l’“orizzonte degli eventi” di un buco nero, dove sono in gioco masse enormi su scale molto ridotte, è necessaria una teoria quantistica della gravità che riesca a gestire il problema degli infiniti. Per risolvere questo genere di difficoltà, nelle teorie quantistiche i fisici si sono inventati la “rinormalizzazione”, una sorta di trucco matematico che permette in un certo senso di assorbire ed eliminare gli infiniti causati dal carattere delle interazioni tra particelle elementari.

Aggirare l’infinito

Nella teorie quantistiche, per determinare il valore di una certa grandezza fisica – per esempio l’energia di una particella o la probabilità di un determinato processo – si può eseguire uno “sviluppo perturbativo”, che consiste nel fare una prima approssimazione grossolana e cercare di renderla sempre più accurata aggiungendo termini di correzione: la grandezza che si vuole calcolare si scompone in una somma di infiniti termini che approssima sempre meglio la quantità cercata, per poi eseguire il calcolo fino alla precisione desiderata. Spesso però tutti i termini di questa somma, a parte il primo, sono infiniti. Quando si lavora con particelle puntiformi, infatti, gli infiniti sono dietro l’angolo. Prendiamo un esempio dall’elettromagnetismo classico: un elettrone può essere rappresentato come una sferetta carica il cui raggio r tende a 0, perché non conoscendone neppure in modo approssimato la struttura interna dobbiamo trattare la particella come un punto. Se cerchiamo di calcolare la sua energia, vediamo però che il risultato diverge: quando r va a 0, l’energia tende all’infinito come 1/r. La rinormalizzazione permette di rimuovere le divergenze che emergono nello sviluppo perturbativo, ridefinendo alcuni parametri con una complessa riformulazione matematica ed esprimendo il calcolo in termini di grandezze misurabili sperimentalmente. Anche se la procedura è piuttosto macchinosa, il trucco funziona bene – alle giuste scale di grandezza – per l’elettromagnetismo, l’interazione nucleare forte e l’interazione nucleare debole. Nel caso della teoria quantistica del campo gravitazionale, però, le divergenze sono ineliminabili. Affinché la teoria sia rinormalizzabile è infatti necessario che tutti gli infiniti che compaiono nei calcoli possano essere assorbiti in un numero finito di parametri liberi e quindi un numero finito di misure e di esperimenti. Con la gravità questo non succede. Per fare previsioni a distanze molto piccole, o a energie molto grandi, occorrerebbero infiniti esperimenti preliminari. La Teoria delle stringhe supera in maniera naturale i problemi dovuti alle divergenze che nascono nel lavorare con particelle puntiformi (cioè prive di dimensioni) perché prende in considerazione oggetti unidimensionali. Non è più necessario un trucco per aggirare gli infiniti che emergono quando il raggio di una particella va a zero, perché la lunghezza della stringa, seppure piccolissima, è sempre maggiore di zero.

La rivoluzione delle stringhe

Storicamente, la Teoria delle stringhe nacque nel 1968 per altri scopi, quando il fisico italiano Gabriele Veneziano rispolverò una funzione matematica, formulata da Eulero e conosciuta da 200 anni, che sembrava descrivere accuratamente alcuni processi nello studio delle interazioni forti, responsabili della coesione dei nuclei atomici. Qualche anno dopo si capì che le interazioni forti sono spiegate da una teoria diversa. Ma le stringhe erano troppo affascinanti per essere messe da parte, e anzi furono riprese con l’ambizione di farne una Teoria del tutto. Ciò che rese particolarmente promettente questa teoria fu l’osservazione che, tra le diverse oscillazioni della stringa, appariva sempre il “gravitone”, quella che si ipotizza essere la particella responsabile delle interazioni gravitazionali. In un certo senso, quindi, la teoria prediceva l’esistenza stessa della gravità, diventando un ottimo candidato come teoria quantistica del campo gravitazionale, la cerniera tra Relatività generale e Meccanica quantistica. Nel corso degli anni la Teoria delle stringhe ha avuto sviluppi tumultuosi, prodotto differenti varianti e generato entusiasmi e delusioni. A metà degli anni Ottanta, durante la “prima rivoluzione delle stringhe”, questo campo coinvolgeva un gran numero di fisici e matematici, intenti a sviluppare dettagli e correzioni per far aderire la matematica e le predizioni che ne emergevano con la realtà fisica conosciuta. Nel momento di massimo fervore, la Teoria delle stringhe, che doveva essere quella unificante di tutta la fisica, risultava però frammentata – con un certo imbarazzo – in ben 5 diverse teorie, tutte prive di verifiche sperimentali dirette o indirette. Fu solo nel 1995, durante la “seconda rivoluzione delle stringhe”, che Edward Witten riuscì a dimostrare che le 5 teorie delle stringhe rappresentavano aspetti diversi di una teoria sovrastante, che chiamò M-teoria. Tuttora non è chiaro il significato della lettera M scelta da Witten: si congettura che possa stare per Matrix, Magic, Mystery oppure anche Mother.

Come in ogni rivoluzione, però, non mancavano i problemi. Molti tentativi di migliorare la teoria e risolvere le contraddizioni esistenti sembravano portare nuove complicazioni. Per esempio si avevano predizioni di particelle mai osservate e c’era bisogno di introdurre ipotesi bizzarre e non verificate sperimentalmente come la “supersimmetria” (motivo per cui spesso di parla di “superstringhe”) e un numero di dimensioni extra. La supersimmetria stabilisce fondamentalmente un nesso tra forze e materia. Secondo la supersimmetria a ogni fermione (le particelle che costituiscono la materia) corrisponderebbe un bosone (le particelle responsabili dei campi di forza) e viceversa: ogni bosone avrebbe un fermione associato. Venne introdotta per far sì che la teoria non prevedesse l’esistenza dei tachioni (particelle con velocità superiori a quelle della luce, vietate dalla Relatività speciale) e riuscisse invece a introdurre i fermioni. Per essere coerente e produrre tutta la fisica che conosciamo, oltre alla supersimmetria la Teoria delle stringhe ha bisogno di ipotizzare l’esistenza di molte più dimensioni rispetto alle 4 consuete a cui siamo abituati: le 3 dimensioni spaziali e quella temporale. Nelle prime versioni della teoria era necessario assumere l’esistenza di ben 26 dimensioni, poi ridotte a 10 nella maggior parte degli sviluppi. Se immaginiamo una stringa in uno spazio unidimensionale, vedremo che può vibrare solo longitudinalmente, estendendosi e contraendosi. Ma se lo spazio diventa un piano a due dimensioni, la stringa potrà vibrare anche trasversalmente. Aumentando le dimensioni, aumenta anche il numero di modi di vibrazione indipendenti. Per descrivere tutti i fenomeni fisici del nostro universo, la teoria richiede una quantità di potenziali modi di vibrazione grande ma precisa, possibile solo in uno spazio-tempo di 10 dimensioni: 9 per lo spazio e una per il tempo. Ma dove sono queste dimensioni, visto che riusciamo a percepirne e misurarne solo 4? La risposta all’enigma è che le dimensioni extra sono “compattificate”, cioè accartocciate su se stesse in spazi troppo piccoli per essere percepiti. Tutti i punti dello spazio-tempo quadridimensionale che osserviamo sarebbero in realtà minuscoli spazi a 6 dimensioni, che noi attraversiamo continuamente senza rendercene conto. Per avere un’idea, immaginiamo un cavo lungo e sottile. Guardandolo da lontano, il cavo sembra una linea, cioè un oggetto unidimensionale. Solo osservandolo da molto vicino si potrebbe apprezzare la sua sezione bidimensionale. Analogamente, le dimensioni extra sarebbero così minute da non essere percepite e sarebbero organizzate e assemblate secondo geometrie particolari.

La forma dello spazio nascosto

Nella Relatività generale è la geometria dello spazio-tempo a determinare la gravità. Analogamente, nella Teoria delle stringhe le geometrie delle dimensioni extra determinano quali particelle esistono, il loro comportamento e le costanti di natura. Oltre a definire il numero di dimensioni necessarie, i fisici avevano bisogno di capire la forma assunta dalle dimensioni extra, di indagare le possibili geometrie degli spazi esadimensionali nascosti e vedere quali avrebbero permesso alle vibrazioni delle stringhe di generare le particelle e le forze osservate sperimentalmente. Un aiuto per provare a dirimere la questione saltò fuori da un recente risultato matematico: le varietà di Calabi-Yau, spazi piccolissimi e compatti, con le giuste caratteristiche, la cui esistenza era stata dimostrata nel 1978 da Shing-Tung Yau, verificando una congettura di Eugenio Calabi risalente al 1954.

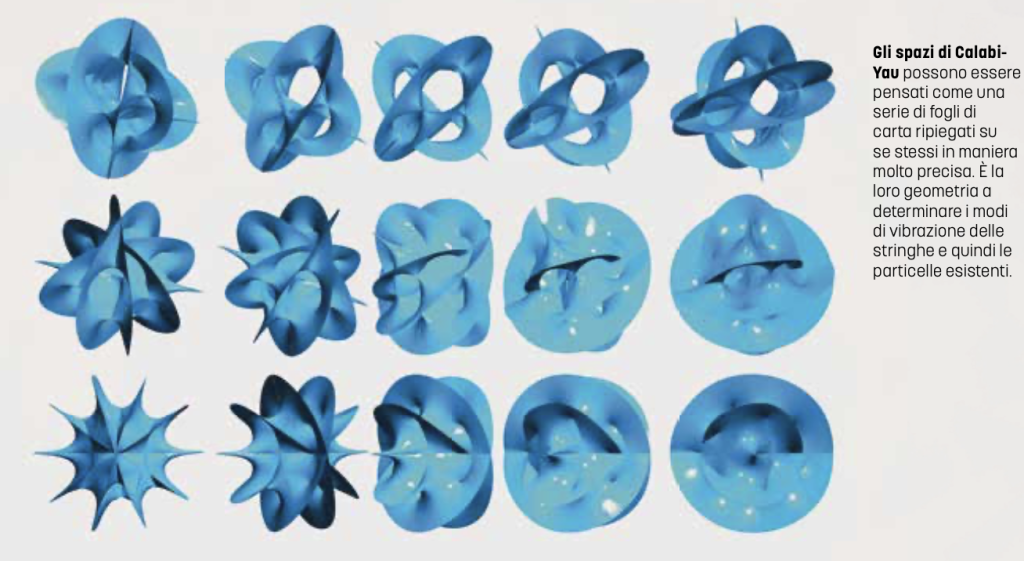
Invece che come un telo esteso infinitamente in tutte le direzioni, una varietà di Calabi-Yau può essere pensata come un foglio di carta ripiegato su se stesso con pieghe molto accurate, che rispondono a leggi precise. Il diametro di questi spazi sarebbe dell’ordine di 10^-32 m, poco sopra la lunghezza di Planck. Un aspetto fondamentale degli spazi di Calabi-Yau è la presenza di buchi. Il numero di buchi di una superficie è una caratteristica molto importante per descriverla. Per esempio una sfera è una superficie bidimensionale senza buchi. Un esempio di superficie con un buco è il toro (la superficie di una ciambella). Cambiando il numero di buchi si ottengono superfici diverse, che non possono essere trasformate le une nelle altre mediante semplici deformazioni, senza strapparne o incollarne dei pezzi. Gli spazi di Calabi-Yau possono avere molti buchi e ognuno può avere più dimensioni. Fisicamente la disposizione precisa dei vari buchi e il modo in cui lo spazio di Calabi-Yau si estende attorno a loro hanno conseguenze precise sui possibili modi di vibrazione delle stringhe. A ogni buco è associata una famiglia di vibrazioni di minima energia, a ciascuna delle quali dovrebbe corrispondere una famiglia di particelle elementari. Di conseguenza, l’esistenza di un certo numero di buchi mostrerebbe che le particelle si suddividono in un numero equivalente di famiglie. Il problema è che gli spazi di Calabi-Yau plausibili sono decine di migliaia, con diversi numeri di buchi e proprietà diverse, e ancora non è stato trovato un criterio per selezionare lo spazio “giusto”, perché le equazioni non ne favoriscono nessuno. Dato che le conseguenze fisiche della Teoria delle stringhe dipendono direttamente dalla scelta della geometria, non è possibile trarre alcuna conclusione definitiva verificabile sperimentalmente, e ciò ne rappresenta il limite principale.

Eredità

Se per mettere a punto la Teoria della gravitazione universale Newton dovette inventare il calcolo infinitesimale, ed Einstein ebbe bisogno della geometria riemanniana – nata da poco – per immaginare lo spazio-tempo necessario alla Teoria della relatività, la Teoria delle stringhe ha attinto a piene mani dalle nuove frontiere della geometria e, viceversa, ha dato nuova linfa alla matematica, permettendo di fornire soluzione a problemi classici che non erano stati risolti con gli strumenti tradizionali. Non sappiamo quale sarà il futuro di questa teoria, che ancora non può vantare nessuna verifica sperimentale. Pur non avendo indizi sull’effettiva esistenza delle stringhe, possiamo però già raccogliere molte idee teoriche nate nell’ambito di questo filone di ricerca. A cinquant’anni dalla sua comparsa sulla scena, la Teoria delle stringhe ha influenzato, arricchito e ispirato le ricerche in moltissimi campi: cosmologia, teoria dell’informazione quantistica, fisica della materia condensata… Ma la disciplina che forse ne ha tratto più vantaggio è proprio la matematica, dove i progressi compiuti resteranno validi indipendentemente dalla bontà fisica delle stringhe.