Giochi matematici – Ma non c’è una soluzione più semplice?

Capita che alcuni nostri lettori talvolta “si arrabbino” quando leggono le soluzioni che i giochisti di Prisma propongono nel dossier dedicato ai giochi matematici. “Si arrabbiano” soprattutto quando trovano la soluzione da noi data troppo pesante e macchinosa, con strumenti da scuole superiori senza che ve ne sia una reale necessità… o almeno questo è quello che ci dicono. Naturalmente a noi il dibattito fa solo piacere e li invitiamo a fornirci le loro soluzioni. In questa rubrica ve le proponiamo, deciderete poi voi lettori quali siano le migliori! Ancora con Maria Dedò!

Gioco 17 (comparso su Prisma 20 di giugno 2020)

UNA FORESTA TRIANGOLARE

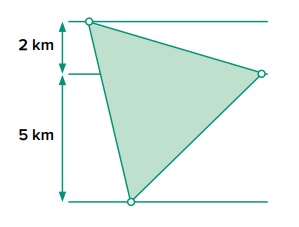
Tre strade parallele passano, ognuna, per uno dei vertici del triangolo equilatero che nel nostro disegno rappresenta la foresta. Tra di loro hanno la distanza indicata in figura. Qual è la lunghezza del lato della foresta? (Se necessario, prendete 1,414 per √2; 1,732 per √3; 2,236 per √5; 3,6056 per √13 e approssimate il risultato al metro più vicino).

Soluzione di Prisma

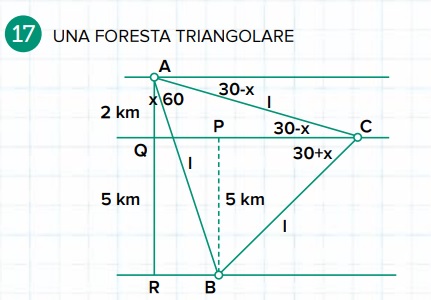
Indicando con x l’angolo RAB e con l la misura dei lati del triangolo equilatero, per il teorema dei triangoli rettangoli, si ha:

1) l cos(x) =7,

2) l sen (30+x)=5

3) l sen(30–x)=2.

Dalla 1) si ricava l=7/cos(x); combinando la 2) e la 3), si trova cos(x)=7/(2√13) e quindi l=2√13 =7,211 km cioè 7211 m.

Soluzione alternativa proposta

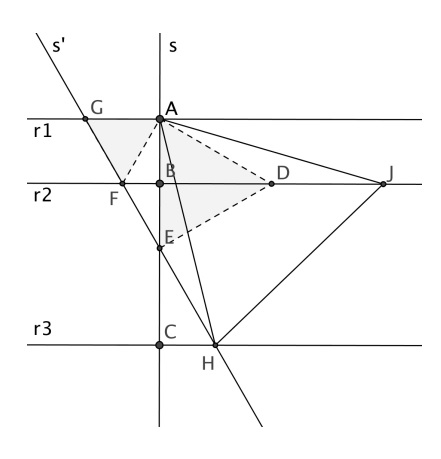
Una soluzione che non usa la trigonometria è la seguente. Con riferimento alla figura in fondo (AB = 2km, BC = 5km) si costruisce:

• un triangolo equilatero ADE tale che E appartenga alla retta s (perpendicolare alle tre rette ri passante per A) e D alla retta r2 (per individuare il punto D basta ruotare la retta s di 60° intorno ad A)
• un triangolo equilatero AFG tale che G appartenga alla retta r1 e F alla retta r2; (analogamente, per individuare F basta ruotare la retta r1 di 60° intorno ad A)

Allora:

• AD=AE=4km (perché BD è altezza e mediana del triangolo equilatero ADE)
• la retta s’ per E e G (che passa per F) si ottiene per rotazione di -60° intorno ad A della retta r2; infatti, E si ottiene per rotazione di -60° intorno a A del punto D e G si ottiene per rotazione di -60° intorno a A del punto F
• AG=AF=(4/√3)km; infatti, l’altezza del triangolo equilatero AFG è uguale alla distanza del punto A dalla retta s’, che a sua volta è uguale alla distanza di A dalla retta r2 cioè ad AB=2km

I triangoli equilateri con un vertice in A, un secondo vertice su r2 e il terzo vertice su r3 sono due, simmetrici rispetto alla retta s: facciamo riferimento a quello dei due che è contenuto nel semipiano che contiene D. Il vertice di tale triangolo che appartiene alla retta r3 si ottiene dal vertice che appartiene a r2 per rotazione di -60° intorno ad A e quindi, oltre a stare su r3, deve appartenere anche alla retta s’ (ottenuta ruotando r2 di -60° intorno ad A).

Quindi questo vertice è il punto H in cui s’ interseca r3 e occorre calcolare la lunghezza di AH, che è il lato del triangolo equilatero con i tre vertici sulle tre rette. I triangoli AEG e CEH sono simili (con rapporto di similitudine EC/EA=3/4). Quindi CH=3AG/4 =√3km e AH = √(AC2+CH2) = √52km ≈ 7,21km.