Il conteggio del contagio

La situazione che attualmente stiamo vivendo nel nostro Paese è, almeno per le presenti generazioni, non soltanto inquietante ma anche inedita. Se gli albori del XXI secolo ci hanno imposto l’abitudine alle misure antiterrorismo, il diffondersi dell’epidemia del coronavirus impone dei cambiamenti immediati nella nostra routine quotidiana, nella nostra zona di conforto, come dicono gli psicologi. Quel che rende più inquieti e rischia di generare panico e comportamenti irrazionali è l’incertezza di ciò che può accadere. La diffusione di un virus, che si trasmette per prossimità e non ha conseguenze così gravi da impedire ai suoi portatori di trasmetterlo ad altri, è un evento impalpabile, non visibile e che spaventa per il suo portato di impredicibilità.

Ma è realmente così? Come tutti i fenomeni incerti e che dipendono da molte variabili, anche i contagi e le epidemie hanno natura “non deterministica” o “stocastica”, come si suole dire, ma questo non implica che non possano essere in qualche modo imbrigliati in un modello matematico. Naturalmente il modello è solo una semplificazione della complessità del fenomeno reale e ha un ambito di applicabilità limitato, ma normalmente offre dei risultati: si pensi alle previsioni del tempo che, sarà vero che oltre tre giorni non sono affidabili ma, al netto di alcune limitazioni, funzionano. Lo stesso vale per i prezzi dei prodotti finanziari e per altri fenomeni apparentemente ingovernabili e irriducibili a regole. Non c’è motivo per non provare quindi a indagare modelli per la diffusione delle epidemie. Intanto facciamo un distinguo: parliamo di “epidemia” per intendere un fenomeno limitato nel tempo, mentre un contagio che si diffonde e si radica in una popolazione si chiama “endemia”. Qui ci limiteremo a discutere i modelli delle epidemie, che non tengono conto del fatto che la diffusione della malattia può avere tempi tali da rendere la fluttuazione della numerosità della popolazione un fattore importante nel modello.

Come costruire un modello per la diffusione di una epidemia? Partiamo dal caso più semplice. Intanto, la prima informazione che vorremmo ottenere è come limitare il contagio, cioè come limitare il numero delle persone infette. Supponiamo di avere un campione di popolazione in cui l’epidemia si diffonde e che possiamo considerare come una popolazione isolata. Dividiamo la popolazione in due parti: il compartimento dei suscettibili (che denotiamo con S) e quello degli infetti (che denotiamo con I). I suscettibili sono le persone non ancora contagiate ma che, appunto, sono suscettibili di esserlo: non appena una di loro si infetta passa dal compartimento S al compartimento I, incrementando il numero I degli infetti mentre riduce il numero S dei suscettibili, secondo lo schema S → I. Quel che ci interessa è stimare l’andamento della variabile I, il numero degli infetti, che cambia da un istante all’altro.

In particolare, ci interessa di quanto si incrementa a ogni istante: infatti, il modello prevede che nel passare da un istante t a un istante successivo t+dt (con dt denotiamo un incremento), il valore di I(t) si incrementi di una quantità dI (che, se negativa, dà in realtà luogo a un decremento). A questo proposito, una assunzione che spesso è ragionevole fare è che questo incremento dI si esprima come:

dI = a × S × I × dt / N

dove N = S + I è la numerosità dell’intera popolazione e la lettera “a” è una costante, la costante di proporzionalità: è come se dicessimo che dI è il 2% di qualcosa. Appare così ragionevole pensare che l’incremento dI sia proporzionale alla numerosità della popolazione dei suscettibili e degli infetti e all’intervallo di tempo preso in considerazione; se uno di questi tre valori raddoppia o triplica, ad esempio, allora anche dI raddoppia o triplica il suo valore.

La definizione di N implica che S = N – I e quindi possiamo riscrivere l’incremento come:

dI = a × (N – I) × I × dt / N

Se supponiamo N costante, questa condizione consente di esprimere il “rapporto incrementale” di I, cioè quanto varia I nell’unità di tempo, come:

dI/dt = a × (N – I) × I / N

Questa equazione dà luogo a quella che si chiama una “equazione differenziale”, in cui al primo membro figura il tasso di crescita di I (la “derivata” di I come dicono i matematici).

Ci sono vari modi per risolvere un’equazione come questa e quindi per riuscire a tracciare il grafico della funzione I al variare di t. Tutti, però, richiedono che sia noto il valore I₀ di I all’istante iniziale t = 0. Noto I₀ e stimato in qualche modo a, abbiamo tutti gli elementi per determinare I, cioè il numero di infetti nel corso del tempo.
Il modello SI fornisce dei grafici del tipo seguente (li rappresentiamo per una popolazione N =1000, con I₀ = 10 e alcuni valori di a):

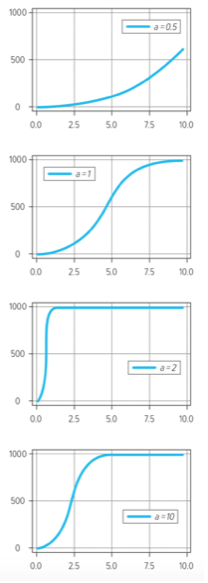
Come si vede (o si intuisce per il primo diagramma pensando di prolungarlo), l’andamento è crescente fino a toccare il massimo, cioè I cresce fino a coincidere con N, ossia l’intera popolazione. Questo modello non lascia scampo: è solo questione di tempo e l’intera popolazione sarà nel compartimento degli infetti! Un modello più realistico consiste nell’introdur- re un ulteriore “compartimento”, quello dei “rimossi” (rappresentato con R), che comprende le persone che sono uscite dal compartimento I degli infetti, in quanto guariti e immuni, o deceduti, o isolati ecc. ma non sono rientrate nel compartimento dei suscettibili. Lo schema diviene quindi S→I→R. La curva R(t), al variare del tempo t, ci interessa in quanto è quella che in qualche modo consente di “svuotare” il compartimento degli infetti. Quest’ultimo, nel modello precedente, era destinato ad aumentare fino ad esaurire l’intera popolazione, invece nel modello SIR, che fu proposto nel 1927 dal biochimico scozzese William Ogilvy Kermack e dal fisico, anche lui scozzese, Anderson Gray McKendrick, l’incremento dI contempla anche un termine negativo che contribuisce quindi a decrementare I(t) e a dare a quest’ultima curva la possibilità di decrescere:

dI = (a × S × I × dt / N) – b × I × dt

Stavolta N = S + I + R e il corrispondente incremento dR risulta essere dR = b × I × dt mentre quello di S è dS = –a × S × I × dt / N. Notiamo infatti che se sommiamo i tre incrementi dS + dI + dR troviamo zero, il che vuol dire che la popolazione totale N rimane invariata. Stavolta abbiamo due parametri, ma il modello ha comunque un comportamento che è deciso da un “teorema della soglia” associato ancora ai nomi di Kermack e McKendrick: se chiamiamo c = a/b, allora è possibile dimostrare che per c > 1 gli infetti aumenteranno fino a raggiungere un picco e poi caleranno lentamente, mentre per c ≤ 1 gli infetti caleranno sempre. Questo numero c del modello SIR si chiama in epidemiologia R₀, ma non va confuso con il valore iniziale R(0) che dà il numero dei rimossi al tempo iniziale. Il numero dei rimossi avrà una dinamica opposta a quella del numero degli infetti, secondo un andamento qualitativo simile a quello indicato nei grafici degli esempi seguenti (che contemplano varie combinazioni di a e di b):

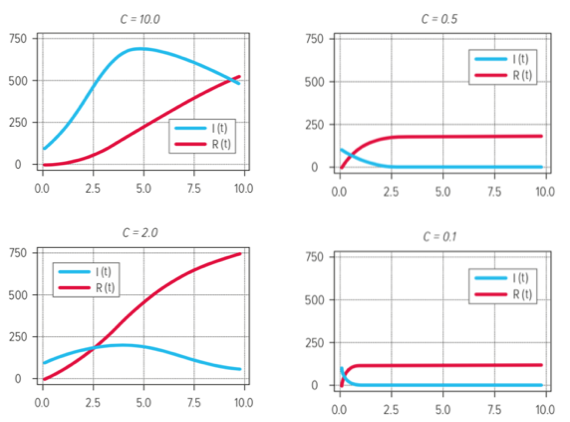
Come si vede, se è c<1, allora la curva degli infetti cala continuamente e quella dei rimossi cresce, fino a “fagocitare” tutti gli infetti. Se invece è c>1, l’epidemia si espande e gli infetti aumentano ma, dopo il raggiungimento di un picco, cominciano a diminuire più o meno bruscamente secondo il valore di c.

Questo in effetti è il comportamento che ci si attende (e si spera!) dalle epidemie, cioè che a un certo punto raggiungano l’apice e poi inizino a divenire meno virulente. Le motivazioni sono molteplici: per esempio, diversi pazienti sviluppano immunità e guariscono, altri muoiono, il virus perde la sua pericolosità in quanto non rappresenta più una novità per i sistemi immunitari della popolazione ecc. Non ultimo, il fatto che si sia riusciti a trovare un vaccino (e speriamo che le vicende che stiamo vivendo abbiano almeno la conseguenza positiva di azzerare la popolazione degli antivaccinisti, piaga oscurantista dei nostri tempi. Si tratta di un compartimento della nostra società che vorremmo veder ridotto non meno di quello degli infetti in un modello epidemiologico!). Come si applicano questi modelli? Come tutti i modelli dati da equazioni differenziali come quelle viste finora, anche SIR è deterministico nel senso che, noto il valore iniziale della funzione che descrive, la soluzione dell’equazione può essere data in corrispondenza di ogni altro istante di tempo.

A noi serve dunque I₀, il valore iniziale degli infetti, che è solitamente disponibile. Ma il modello dipende anche da due parametri, a e b. Senza poter attribuire loro un valore non possiamo tracciare una curva specifica per la soluzione dell’equazione e, come i diagrammi precedenti hanno mostrato, a seconda dei valori dei parametri le curve possono cambiare anche dal punto di vista qualitativo, non solo quantitativo. Quel che serve è quindi “calibrare” il modello pensando ai modelli matematici come a degli abiti. Anche se sappiamo fabbricare un paio di pantaloni, non riusciremo a farli calzare su una particolare persona se non ne conosciamo le caratteristiche fisiche, che spesso sono condensate in un parametro, la taglia fra gli altri: così, un paio di pantaloni di taglia 50 non potrà adattarsi a qualcuno che porta la 52.

Analogamente dobbiamo trovare la “taglia” del modello, cioè stimare i parametri relativi a una determinata epidemia. Per farlo si usano i dati reali disponi- bili. Per esempio, supponiamo di conoscere i valori di S, I, R e N per un certo intervallo temporale: potremmo, per dirne una, aver ascoltato i bollettini della protezione civile ogni giorno e annotato i valori. I è il numero dei casi positivi ancora in vita, R il numero di deceduti e guariti, N il numero di persone cui è stato fatto il tampone, e S = N – R – I.

Ecco il grafico con alcuni valori percentuali relativi agli infetti da Covid19 in Italia fra fine febbraio e inizio marzo:

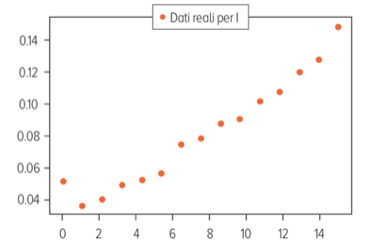
Abbiamo una serie di 15 rilevazioni a un giorno di distanza le une dalle altre: il nostro I₀ è sicuramente il primo dato della serie mentre, per determinare a e b, possiamo operare una “ottimizzazione”, vale a dire provare a cercare questi due valori in modo che, sostituiti nell’equazione differenziale, rendano la curva della sua soluzione la più possibile vicina a tutti i punti della serie contemporaneamente. Ecco alcune curve per diversi valori di a e b:

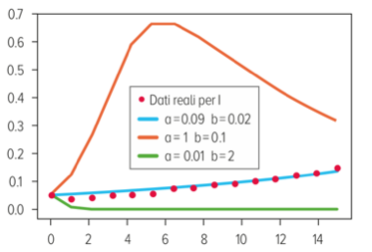
Come si vede, i valori a = 0.09 e b = 0.02 danno luogo a una curva (quella blu) che approssima molto bene i valori reali, laddove le altre due curve desunte dalla stessa equazione per valori diversi dei parametri hanno un comportamento del tutto diverso e sembrano avere poco o nulla a che fare con i dati reali. Una volta determinati i parametri con un procedimento di ottimizzazione, il modello offre una soluzione univoca che, si spera, sia in grado di offrire l’andamento del numero degli infetti nell’immediato futuro. Per esempio, ecco le curve a 180 giorni dei valori di S, I e R dopo la calibrazione appena illustrata (a=0.09 e b=0.02): sulle ordinate è indicata la percentuale di infetti in una popolazione costante.

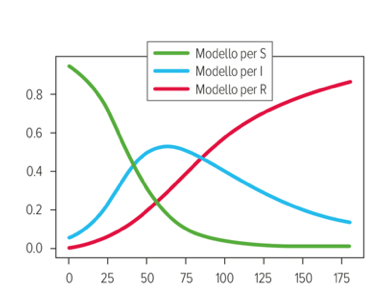
Come ci aspettiamo, c’è un picco massimo dell’epidemia corrispondente al massimo della curva blu degli infetti; dopo, questo numero decresce lentamente. Va specificato che queste calibrazioni devono essere ripetute perché, sebbene il modello supponga a e b costanti, in realtà questi parametri variano nel tempo e la loro stima condotta con una nuova ottimizzazione consente di migliorare la predittività del modello “in corso d’opera”.

Naturalmente esistono modelli più complessi del SIR, con altri compartimenti, ma i meccanismi della matematica delle epidemie sono quelli che abbiamo qui descritto. Speriamo che l’unica cosa contagiosa rimanga la voglia di approfondire questi affascinanti argomenti di matematica applicata!