La pioggia nel pi greco

di Paolo Caressa

Tutti abbiamo sentito parlare del “pi greco” fin da bambini, quando a scuola ci sono stati dati i rudimenti del calcolo di circonferenze, aree e volumi. Chi non ricorda la regoletta “raggio per raggio per tre e quattordici” oppure “due pi greco erre” per l’area e la lunghezza della circonferenza di un cerchio? Forse c’è anche chi ricorda la “quattro terzi pi greco erre tre” per il volume della sfera!

In effetti queste formule erano parzialmente conosciute nel mondo antico e completamente note in quello ellenistico: Archimede, il più grande matematico dell’antichità e forse dell’intera storia umana, le dimostra e le utilizza nelle sue opere su aree e volumi dei solidi, in special modo  nel suo straordinario tour de force sulla sfera e sul cilindro. In particolare, fornisce un metodo generale per calcolare pi greco con la precisione voluta, tanto che questo numero è noto anche come numero di Archimede.

L’origine dell’uso sistematico della lettera greca π è però recente. Il primo grande matematico a farne uso fu Eulero che, a dire il vero, con π indicava il rapporto fra circonferenza e raggio e non fra circonferenza e diametro (quindi intendeva la costante che oggi si chiama τ, tau, e che molti propongono di sostituire a pi greco come costante universale).

Forse, dagli anni di scuola, ci ricordiamo anche che pi greco non è un numero razionale, cioè non esiste  coppia di interi n e m tale che valga la relazione π = n/m. Ma se non è il rapporto di alcuna coppia di numeri interi, il suo sviluppo decimale è infinito non periodico e quindi la formuletta “raggio per raggio per tre e quattordici” fornisce soltanto una approssimazione dell’area del cerchio, approssimazione che deriva dal prendere le sole prime due cifre decimali dello sviluppo di pi greco.

ACQUISTA PRISMA IN PDF

Naturalmente gli antichi ignoravano i numeri irrazionali. In fondo, per i loro scopi questa mancanza non rappresentava un reale impedimento allo sviluppo tecnologico e ingegneristico: gli Egizi usavano il valore (16/9)² pari a circa 3,16 e i Babilonesi utilizzavano 25/8 = 3,125 come valore per i loro calcoli. Dal canto suo, Archimede non pretende di trovarne il valore, ancorché approssimato, ma dimostra che il numero pi greco è maggiore di 223/71 (all’incirca 3,1408) e minore di 22/7 (all’incirca 3,1429).

Oggi possiamo interrogare una qualsiasi calcolatrice, computer o cellulare e trovare una sbrodolata di cifre di pi greco più che sufficienti per qualsiasi scopo concreto: dal XVII secolo in poi numerosi matematici hanno trovato formule in grado di produrre tutte le cifre di pi greco in un tempo infinito e quindi utilizzabili per produrne con una precisione voluta (molti di questi procedimenti coinvolgono i cosiddetti “sviluppi in serie”). Ma nel XVIII secolo fu inventato un modo nuovo di calcolare pi greco, che in realtà si applica fruttuosamente in moltissimi altri campi, e che qui descriveremo in una variante più semplice di quella escogitata nel 1733 dal suo creatore, Georges-Louis Leclerc, conte di Buffon.

Il nostro metodo richiede un enorme foglio di carta, una matita e… la pioggia. Supponiamo infatti di ritagliare un foglio di carta o cartone, ricavandone un quadrato di due metri per lato, e di inscrivervi un cerchio, che così tocca in quattro parti il quadrato, precisamente nei punti medi di ciascun suo lato. In particolare, il raggio del cerchio è la metà del lato del quadrato, dunque il cerchio ha raggio uno.

Poiché la regoletta dell’area del cerchio afferma che il quadrato del raggio per pi greco fornisce l’area del cerchio (in formule:  A=r×r×π) e, nel nostro caso il raggio vale uno, abbiamo: A=π.

Quindi l’area del cerchio è proprio il valore che vogliamo determinare. Ora, notiamo che l’area del quadrato dove il cerchio è inscritto è il quadrato del lato che misura 2 metri, quindi l’area del quadrato è di 4 metri quadrati. Mettiamo infine il nostro foglio sotto la pioggia e aspettiamo un po’: supponiamo, come è ragionevole che sia, che le gocce tendano a cadere a caso in modo uniforme all’interno del quadrato (in effetti, se usciamo sotto la pioggia senza ombrello, dopo un po’ saremo tutti bagnati; non solo sulla spalla destra, per esempio). Supponiamo inoltre di riuscire, una volta tirato il foglio dentro casa, a contare le gocce: per esempio, il cartone potrebbe essere colorato in modo che la goccia sia distinguibile per il colore che imprime al cartone. Dunque, immaginiamo di poter calcolare, semplicemente contando, i due seguenti numeri:

• C =  numero di gocce cadute soltanto nel cerchio
• Q =  numero di gocce cadute in tutto il quadrato.

La nostra ipotesi ragionevole, in merito al fatto che le gocce cadano democraticamente in qualsiasi parte del quadrato in modo casuale, implica che il rapporto Q/C tende sempre di più ad approssimare il rapporto Area del quadrato/Area del cerchio. Ma quest’ultimo rapporto è proprio 4/π per cui, al crescere del numero di gocce totali, abbiamo che Q/C è una approssimazione sempre migliore di 4/π e quindi che C/Q è una approssimazione sempre migliore di π/4. Da qui segue che 4 × C/Q è una approssimazione sempre migliore di π. Pertanto possiamo approssimare

Ai tempi di Buffon questa formula costituiva poco più che una curiosità matematica: oggi invece è facilissimo simulare al computer la caduta delle gocce di pioggia all’interno del quadrato, visto che i computer possono estrarre numeri (quasi) a caso.

Un esempio è dato dalla seguente figura, che illustra una semplice simulazione programmata dall’autore.

In questo caso sono state simulate 1000 gocce e il programma per ciascuna di loro ha verificato se cadeva all’interno del cerchio (colorandola in blu anziché celeste), ottenendo il seguente valore: 785 sono effettivamente cadute all’interno del cerchio. Applicando la formula precedente troviamo

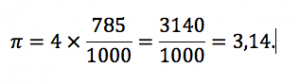Naturalmente, ripetendo lo stesso esperimento, non si trova mai lo stesso numero esatto di gocce cadute all’interno del cerchio (sarebbe strano il contrario, dato che usiamo un processo non deterministico che comporta l’uso di numeri a caso) ed è evidente che, aumentando il numero di gocce totali, aumenta anche la precisione del calcolo. In particolare la scelta dei 785 punti è stata un po’ fortunata e “giocando” con il programma di simulazione si vede abbastanza bene che con 1000 gocce si riesce a determinare solo la prima cifra decimale (l’1 dopo la virgola).

Per determinare la seconda cifra decimale (il 4), dopo un po’ si nota che servono un milione di simulazioni. In altri termini, la precisione della determinazione di pi greco con il metodo di Buffon cresce molto lentamente, all’incirca con il crescere della radice quadrata del numero totale di gocce di pioggia.

ABBONATI A PRISMA

Ma la semplicità del metodo e la facilità di programmarlo su un elaboratore hanno fatto sì che duecento anni dopo Buffon sia stato riscoperto e applicato per calcoli più drammaticamente concreti. In particolare, nei calcoli necessari per la costruzione della prima bomba atomica, negli anni ’40. Infatti lo stesso principio per cui un rapporto di aree viene approssimato con un conteggio consente di calcolare degli oggetti matematici chiamati “integrali definiti”, che pervasivamente popolano ogni ramo della scienza e della tecnica. Il primo ad aver applicato tali metodi in questo ambito più generale, ma in lavori non pubblicati, è stato Enrico Fermi negli anni ’30. Tuttavia il merito della loro diffusione va ascritto a Stanislaw Ulam e a John von Neumann, che programmò il metodo sul calcolatore ENIAC, uno dei primi computer della storia, operativo dal 1946. All’epoca, queste ricerche erano top secret e ad esse fu dato un nome in codice, che è poi quello che ancora si usa per denotarle: metodo di Monte Carlo (con allusione al casinò e quindi alla casualità insita nel processo). Oggi il metodo di Monte Carlo trova applicabilità universale ed è programmato per risolvere problemi di fisica, ingegneria, chimica, economia e finanza, meteorologia, biologia e chi più ne ha più ne metta. Non male per una boutade matematica scoperta… per caso da un nobile del ‘700.

da Prisma n.5 | Marzo 2019